Оценка одного параметра

Пусть задана плотность распределения 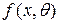с одним параметром. Согласно методу моментов приравниваем, например, соответствующие начальные моменты первого порядка, т.е. среднюю выборки 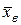и математическое ожидание распределения .

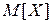Здесь достаточно одного уравнения относительно этого параметра:

. (*)

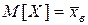Поскольку математическое ожидание является функцией параметра :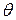

,

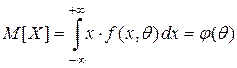соотношение (*) можно рассматривать как уравнение с одним неизвестным, которое определяет точечную оценку параметра 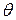, являющуюся функцией.