ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Практикум
СОДЕРЖАНИЕ
| ВЕРОЯТНОСТЬ. ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ…………...………………..... | |
| 1. Пространство элементарных событий. Операции над случайными событиями ……………….…...... | |
| 2. Элементы комбинаторики. Непосредственный подсчет вероятностей.............................................. | |
| 3. Геометрические вероятности …………....……..... | |
| 4. Теоремы сложения и умножения вероятностей | |
| 5. Формула полной вероятности и формула Байеса | |
| 6. Повторные независимые испытания (схема Бернулли) …….............................................………….. | |
| СЛУЧАЙНЫЕ ВЕЛИЧИНЫ ….......……………….... | |
| 7. Дискретная случайная величина ………......…... | |
| 8. Непрерывные случайные величины. Плотность вероятности ……...............................................…... | |
| 9. Закон больших чисел …………......…………….... | |
| 10. Распределение функции одного и двух случайных аргументов ……............................................... | |
| ПРИЛОЖЕНИЯ …………………………………….... | |
| ЛИТЕРАТУРА ………………………………………... |
ВЕРОЯТНОСТЬ.
ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
1. Пространство элементарных событий.
Операции над случайными событиями
В основе теории вероятностей лежит понятие случайного эксперимента. Эксперимент считается случайным, если он может закончиться любым из совокупности известных результатов, но до осуществления эксперимента нельзя предсказать, каким именно.
Примеры случайного эксперимента: бросание монеты, игральной кости, проведение лотереи, азартные игры, стрельба по цели, поступление звонков на телефонную станцию и т.п.
Различные результаты эксперимента называют исходами.
Определение 1. Множество всех взаимоисключающих исходов эксперимента называется пространством элементарных событий. Взаимоисключающие исходы — это те, которые не могут наступить одновременно.
Пространство элементарных событий будем обозначать буквой Ω, а его исходы — буквой ω.
Определение 2. Произвольное подмножество пространства элементарных событий называется событием. Событие может состоять из одного или нескольких элементарных событий, а также из счетного или несчетного числа элементарных событий.
Событие Ω, состоящее из всех исходов эксперимента, называется достоверным событием. Оно обязательно происходит, так как эксперимент всегда заканчивается каким-нибудь исходом.
Пустое множество исходов эксперимента называется невозможным событием и обозначается символом ø.
Определение 3. Суммой двух событий А и В (обозначается 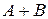 ) называется событие, состоящее из всех исходов, входящих либо в А, либо в В. Другими словами, под
) называется событие, состоящее из всех исходов, входящих либо в А, либо в В. Другими словами, под 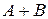 понимают следующее событие: произошло или событие А, или событие В, либо они произошли одновременно, т.е. произошло хотя бы одно из событий А или В (рис. 1.1а).
понимают следующее событие: произошло или событие А, или событие В, либо они произошли одновременно, т.е. произошло хотя бы одно из событий А или В (рис. 1.1а).
Определение 4. Произведением двух событий А и В (обозначается АВ) называется событие, состоящее из тех исходов, которые входят как в А, так и в В. Иными словами, АВ означает событие, при котором события А и В наступают одновременно (рис. 1.1б).
Определение 5. Разностью двух событий А и В (обозначается 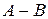 ) называется событие, состоящее из исходов, входящих в А, но не входящих в В.
) называется событие, состоящее из исходов, входящих в А, но не входящих в В.
Смысл события 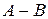 состоит в том, что событие А наступает, но при этом не наступает событие В (рис. 1.1в).
состоит в том, что событие А наступает, но при этом не наступает событие В (рис. 1.1в).
Определение 6. Противоположным(дополнительным) для события А (обозначается 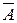 ) называется событие, состоящее из всех исходов, которые не входят в А. Наступление события
) называется событие, состоящее из всех исходов, которые не входят в А. Наступление события 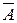 означает просто, что событие А не наступило.
означает просто, что событие А не наступило.
Если события изобразить на плоскости, то результат определенных операций над событиями выглядит следующим образом:

Рис. 1.1
Определение 7. События А и В называются несовместимыми, если нет исходов, входящих как в А, так и в В, т.е. АВ = ø.
Определение 8. Говорят, что событие А содержится в событии В (обозначается 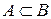 ), если все исходы события А входят в событие В.
), если все исходы события А входят в событие В.
Свойства операций над событиями
1) 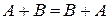 ; ; | 2) 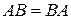 ; ; | 3) 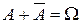 ; ; |
4) 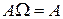 ; ; | 5) 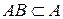 ; ; | 6) 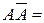 ø; ø; |
7) 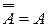 ; ; | 8) 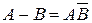 ; ; | 9) 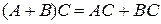 ; ; |
10) 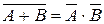 ; ; | 11) 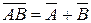 ; ; | 12) 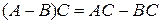 . . |
Пример 1.1. Два шахматиста играют подряд две партии. Под исходом опыта будем понимать выигрыш одного из них в i -й партии или ничью. Построить пространство 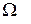 элементарных исходов.
элементарных исходов.
Решение. Обозначим события 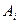 — в i -й партии выиграл первый игрок,
— в i -й партии выиграл первый игрок, 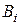 — второй, С — ничья. Тогда возможные исходы игры:
— второй, С — ничья. Тогда возможные исходы игры:
1. Обе партии выиграл первый игрок 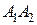 .
.
2. Обе партии выиграл второй игрок 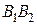 .
.
3. Обе партии закончились вничью 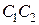 .
.
4. В первой партии выиграл первый игрок, во второй — второй 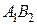 .
.
5. В первой выиграл первый игрок, во второй — ничья 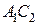 .
.
6. В первой партии победа второго игрока, во второй — первого 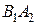 .
.
7. В первой — победа второго игрока, во второй — ничья 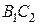 .
.
8. В первой — ничья, во второй — победа первого игрока 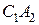 .
.
9. В первой — ничья, во второй — победа второго игрока 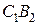 .
.
Ответ: 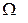 =
= 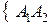 ,
, 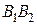 ,
, 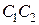 ,
, 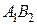 ,
, 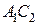 ,
, 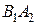 ,
, 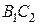 ,
, 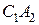 ,
, 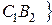 .
.
Пример 1.2. Пусть А, В, С — три произвольных события. Найти выражения для событий, состоящих в том, что из А, В, С:
1. Произошло только А.
2. Произошло А и В, но С не произошло.
3. Все три события произошли.
4. Произошло, по крайней мере, одно из событий.
5. Произошли, по крайней мере, два события.
6. Произошло одно и только одно событие.
7. Произошли два и только два события.
8. Ни одно событие не произошло.
9. Произошло не более двух событий.
 2015-04-08
2015-04-08 742
742







