Простая и логически ясная модель временного ряда имеет следующий вид:
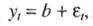 (11.5)
(11.5)
где b — константа, а ε — случайная ошибка. Константа b относительно стабильна на каждом временном интервале, но может также медленно изменяться со временем. Один из интуитивно ясных способов выделения значения b из данных состоит в том, чтобы использовать сглаживание скользящим средним, в котором последним наблюдениям приписываются большие веса, чем предпоследним, предпоследним большие веса, чем пред- предпоследним, и т.д. Простое экспоненциальное сглаживание именно так и построено. Здесь более старым наблюдениям приписываются экспоненциально убывающие веса, при этом, в отличие от скользящего среднего, учитываются все предшествующие наблюдения ряда, а не только те, которые попали в определенное окно. Точная формула простого экспоненциального сглаживания имеет вид:
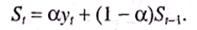 (11.6)
(11.6)
Когда эта формула применяется рекурсивно, каждое новое сглаженное значение (которое является также прогнозом) вычисляется как взвешенное среднее текущего наблюдения и сглаженного ряда. Очевидно, результат сглаживания зависит от параметра α. Если α равен 1, то предыдущие наблюдения полностью игнорируются. Если а равен 0, то игнорируются текущие наблюдения. Значения α между 0 и 1 дают промежуточные результаты. Эмпирические исследования показали, что простое экспоненциальное сглаживание весьма часто дает достаточно точный прогноз.
На практике обычно рекомендуется брать α меньше 0,30. Однако выбор а больше 0,30 иногда дает более точный прогноз. Это значит, что лучше все же оценивать оптимальное значение α по реальным данным, чем использовать общие рекомендации.
На практике оптимальный параметр сглаживания часто ищется с использованием процедуры поиска на сетке. Возможный диапазон значений параметра разбивается сеткой с определенным шагом. Например, рассматривается сетка значений от α =0,1 до α = 0,9 с шагом 0,1. Затем выбирается такое значение α, для которого сумма квадратов (или средних квадратов) остатков (наблюдаемые значения минус прогнозы на шаг вперед) является минимальной.
Microsoft Excel располагает функцией Экспоненциальное сглаживание (Exponential Smoothing), которая обычно используется для сглаживания уровней эмпирического временного ряда на основе метода простого экспоненциального сглаживания. Для вызова этой функции необходимо на панели меню выбрать команду Tools - Data Analysis. На экране раскроется окно Data Analysis, в котором следует выбрать значение Экспоненциальное сглаживание. В результате появится диалоговое окно Экспоненциальное сглаживание, представленное на рис. 11.5.
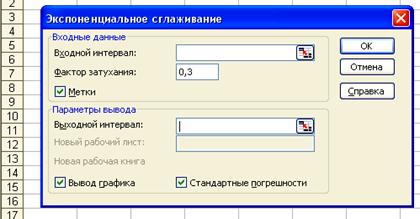
В диалоговом окне Exponential Smoothing задаются практически те же параметры, го и в рассмотренном выше диалоговом окне Moving Average.
1. Input Range (Входные данные) — в это поле вводится диапазон ячеек, содержащих значения исследуемого параметра.
2. Labels (Метки) — данный флажок опции устанавливается в том случае, если первая строка (столбец) во входном диапазоне содержит заголовок. Если заголовок отсутствует, флажок следует сбросить. В этом случае для данных выходного диапазона будут автоматически созданы стандартные названия.
3. Damping factor (Фактор затухания) — в это поле вводится значение выбранного коэффициента экспоненциального сглаживания α. По умолчанию принимается значение α = 0,3.
4. Output options (Параметры вывода) — в этой группе, помимо указания диапазона ячеек для выходных данных в поле Output Range (Выходной диапазон), можно также потребовать автоматически построить график, для чего необходимо установить флажок опции Chart Output (Вывод графика), и рассчитать стандартные погрешности, для чего нужно установить флажок опции Standart Errors (Стандартные погрешности).
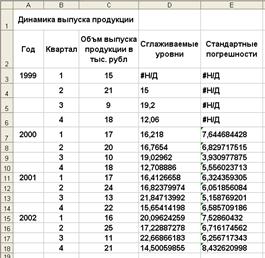
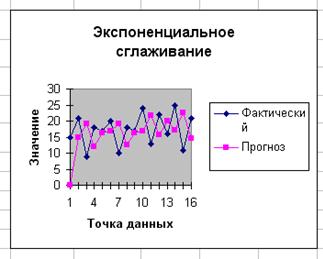
Воспользуемся функцией Экспоненциальное сглаживание для повторного решения рассмотренной выше задачи, но уже с помощью метода простого экспоненциального сглаживания. Выбранные значения параметров сглаживания представлены на рис. 11.5. На рис. 11.6 показаны рассчитанные показатели, а на рис. 11.7 — построенные графики.
 2015-04-08
2015-04-08 3599
3599
