Сглаживание временных рядов

Сглаживание временных рядов – это выделение основной тенденции 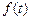из состава динамического ряда, который кроме нее содержит случайную составляющую 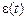. Применяют различные математические способы сглаживания.

Во-первых, это аналитическое сглаживание. Данный метод аналогичен традиционному МНК, который используется для оценки параметров уравнений регрессии (п.1.2). Реализуя соответствующий алгоритм, необходимо учитывать единственное отличие тренда от регрессии, заключающееся в том, что в качестве независимой переменной в трендовых моделях рассматривается время .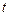

Данный подход считается наиболее точным по сравнению с остальными. Его основное преимущество проявляется в том, что он позволяет построить модель временного ряда, а не ограничиться исследованием его числовых значений.

Одним из наиболее распространенных приемов сглаживания является метод скользящих средних. Вместо фактических уровней ряда в данном случае используются его средние значения, рассчитанные за определенный интервал сглаживания 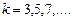. Длина интервала предполагается, таким образом, равной нечетному количеству уровней исходного ряда. Найденное среднее значение относится к середине интервала сглаживания, далее наблюдения сдвигаются на один уровень вперед и расчеты повторяются.

Недостатки этого способа связаны с потерей части исходной информации. Кроме того, интервал сглаживания может совпадать с циклом сезонных или периодических колебаний. Поэтому применяется модификация данного способа, а именно, способ взвешенных скользящих средних, в соответствии с которым для каждого интервала сглаживания с помощью МНК строится полиномиальное уравнение тренда.

Принципиально важными преимуществами по сравнению с другими методами выделения тренда обладает экспоненциальное сглаживание (метод Брауна). Сущность этого метода раскрывают его основные характеристики – экспоненциальные средние. В частности, экспоненциальная средняя k -го порядка для ряда длиной в n уровней обозначается как .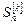

Эти средние учитывают различия в степени влияния ретроспективных уровней ряда на его прогнозные значения, а именно, уменьшение значимости уровней от конца временного ряда к его началу по экспоненте. Данное свойство ряда моделируется с помощью параметра сглаживания 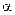, значения которого изменяются в пределах от 0 до 1. Сглаживание с помощью экспоненциальных средних позволяет, следовательно, учесть всю информацию, т.е. все уровни сглаживаемого динамического ряда.

Экспоненциальная средняя первого порядка рассчитывается следующим образом:

.

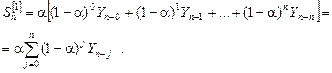Выбор 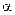влияет на точность расчетов и осуществляется в зависимости от того, насколько быстро будут снижаться веса предшествующих наблюдений и степень их влияния на сглаживаемый уровень, т.е., чем больше 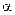, тем меньше влияние предшествующих уровней. Средний уровень 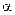обычно принимается равным 0,35. В общем случае

,

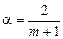где m - число уровней, входящих в интервал сглаживания.

Экспоненциальные средние различных порядков связаны друг с другом рекуррентным соотношением, которое в практических расчетах выглядит как

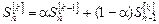. (4.12)

Принято в качестве допущений, что 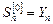. Начальные значения экспоненциальных средних определяются в зависимости от уравнения тренда, выбранного по результатам аналитического сглаживания. Например, для линейного уравнения тренда 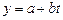они будут определяться согласно формулам вида

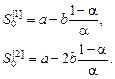(4.13)

Если тенденцию развития экономического процесса нельзя описать одной функцией 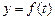на всем промежуткеизменения величины 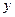, то ее целесообразно представить в виде сплайн-функции, частным случаем которых являются функции, аппроксимирующие четвертый тип экономического развития (п. 4.4.1).

Сплайн-функция – это кусочно-гладкая функция, отдельные участки которой соединены гладким образом. В качестве отрезков выбираются полиномы различной степени. В этом случае внутри каждого отрезка тенденция процесса будет описываться более простой функцией, что способствует лучшему анализу данного процесса.

Полиномиальным сплайном степени 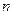называется составленная из полиномов степени не выше 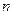непрерывная кусочная полиномиальная функция, производные которой до порядка 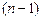включительно непрерывны. Например, полиномиальный сплайн первой степени (линейный сплайн) представляет собой непрерывную кусочно-линейную функцию, зависящую от времени t, если ось времени .

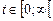Этот интервал разделяют на 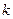участков (частей): 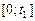, , 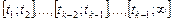каждый из которых представляет собой прямую, а весь сплайн состоит из совокупности линейных отрезков в количестве 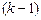и луча. Уравнение такого сплайна имеет следующий вид:

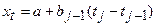, (4.14)

где , ;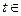

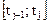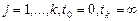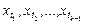– точки перелома (стыковки).

Время 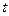заменяется новыми переменными

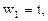
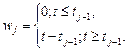
С учетом новых переменных линейный сплайн записывается следующим образом:

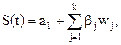(4.15)

в котором

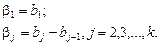
Коэффициент 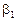есть угловой коэффициент сплайна над первым интервалом, а остальные коэффициенты 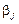, начиная с 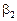, показывают изменение углового коэффициента при переходе от интервала 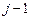к интервалу 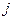соответственно.

Применение линейных сплайнов имеет ряд преимуществ по сравнению с полиномиальными сплайнами более высоких степеней.

Во-первых, он имеет очевидную экономическую интерпретацию – рост с кусочно-постоянными абсолютными приростами. Во-вторых, его включение в более общие динамические модели позволяет использовать достаточно простой математический аппарат – линейную алгебру, линейное программирование.