Вычисление площадей при параметрическом задании функции

Пусть криволинейная трапеция ограничена линиями x=a, x=b, y=0, а верхняя граница задана параметрически 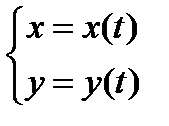. Как известно, площадь криволинейной трапеции равна S= 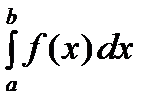= = 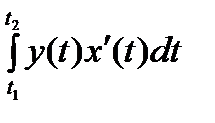S, так как dx=x¢(t)×dt, f(x)=y(t). Причем нижний предел интегрирования t₁ соответствует точке x=a; x(t₁)=a, верхний предел интегрирования t₂ соответствует точке x=b; x(t₂)=b.

Пример: Вычислить площадь, ограниченную эллипсом. Параметрические уравнения эллипса: .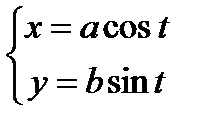

В силу симметричности фигур вычислим 1/4 площади, расположенную в первой четверти. Для этой части x меняется от 0 до a. Найдем пределы интегрирования.

0 = a cos t, cos t = 0, t₁=p/2,

a = a cos t, cos t = 1, t₂ = 0.

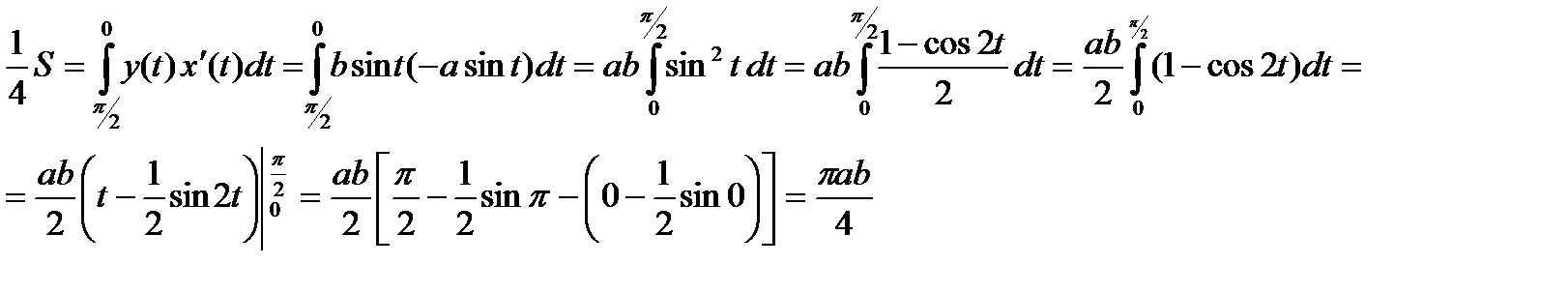
Итак, 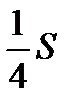=pab/4 Þ S= pab (ед²).