Если в декартовой системе координат вычисляется площадь криволинейной трапеции, то в полярной системе вычисляется площадь криволинейного сектора.
Определение: Криволинейным сектором называется фигура, заключенная между двумя лучами, выходящими из полюса под углами j=a и j=b и кривой, заданной в полярной системе координат r=r(j).
Разобьем криволинейный сектор лучами j=ji, i = 0…n на части
a=j0<j1<j2<…<jn=b
j =a, j =b, r =r(j).
| a |
| b |
| r=r(j) |
В каждой части произвольным образом выбираем точку Ci и вычисляем в ней значение ri =r(Ci) угол i - части 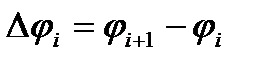 . Заменим площадь i - части площадью кругового сектора
. Заменим площадь i - части площадью кругового сектора 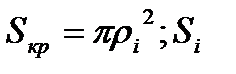 =
= 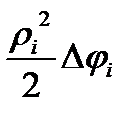
Просуммируем площади всех круговых секторов 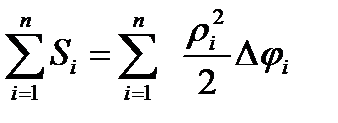 .
.
Сумма этих площадей приближенно равна площади исходного криволинейного сектора. Причем, чем больше будет частей разбиения, тем меньше будет Dji, тем точнее будет равенство.
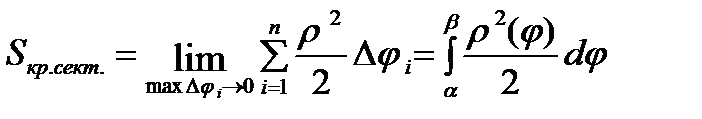
В ПСК: S= 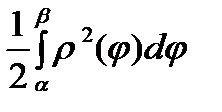 .
.
 2015-04-12
2015-04-12 2368
2368
