1) Пусть плоская фигура представляет собой криволинейную трапецию
 то есть фигуру, ограниченную линиями
то есть фигуру, ограниченную линиями 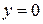 ,
, 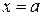 ,
, 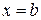 ,
, 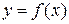 , где
, где  – непрерывна на отрезке
– непрерывна на отрезке  и
и 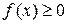 . Тогда ее площадь находится по формуле
. Тогда ее площадь находится по формуле 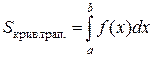 .
.
2) Пусть фигуру можно разбить на две криволинейные трапеции: под графиком 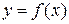 на отрезке
на отрезке  и под графиком
и под графиком 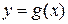 на отрезке
на отрезке 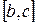 . Тогда ее площадь вычисляется по формуле
. Тогда ее площадь вычисляется по формуле
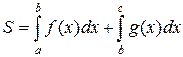 .
.
Пример. Вычислить площадь сектора с углом 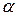 и радиусом
и радиусом 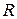 .
.
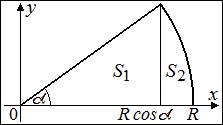 Расположим сектор на координатной плоскости так, чтобы его вершина находилась с начале координат, и один из его радиусов лежал в положительной части оси
Расположим сектор на координатной плоскости так, чтобы его вершина находилась с начале координат, и один из его радиусов лежал в положительной части оси  . Тогда сектор можно разбить на две криволинейные трапеции, соответственно его площадь
. Тогда сектор можно разбить на две криволинейные трапеции, соответственно его площадь 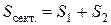 .
.
Здесь первое слагаемое является площадью криволинейной трапеции под графиком линейной функции 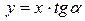 и вычисляется по формуле
и вычисляется по формуле
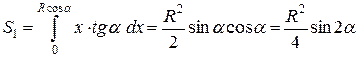 .
.
Второе слагаемое представляет собой площадь под дугой окружности, задаваемой уравнением 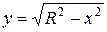 . Вычислим эту площадь:
. Вычислим эту площадь:
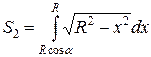 .
.
Сделаем в интеграле замену переменной 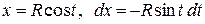 .
.
Пересчитаем пределы интегрирования: при 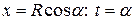 ; при
; при
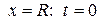 . Подставляя
. Подставляя  в интеграл, получаем
в интеграл, получаем
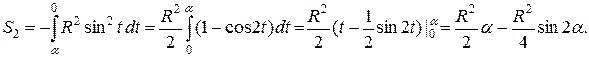
Складывая две вычисленные площади, находим площадь сектора
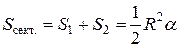 .
.
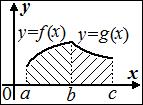
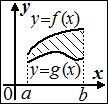 3) Пусть плоская фигура ограничена: сверху - графиком функции
3) Пусть плоская фигура ограничена: сверху - графиком функции 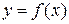 ,
,  ; снизу - графиком функции
; снизу - графиком функции 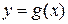 ,
,  ; по бокам - вертикальными отрезками
; по бокам - вертикальными отрезками 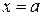 и
и 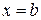 , которые могут вырождаться в точку. Тогда площадь этой фигуры равна разности площадей соответствующих криволинейных трапеций и вычисляется по формуле
, которые могут вырождаться в точку. Тогда площадь этой фигуры равна разности площадей соответствующих криволинейных трапеций и вычисляется по формуле
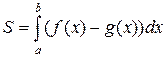 .
.
Пример. Найти площадь фигуры, ограниченной линиями 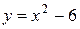 и
и 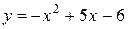 .
.
Найдем сначала абсциссы точек пересечения графиков данных функций. Для этого решаем систему уравнений
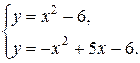
Отсюда находим 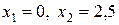 . Искомая площадь вычисляется по формуле
. Искомая площадь вычисляется по формуле
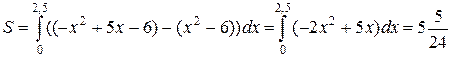 .
.
 2015-05-05
2015-05-05 4141
4141
