Теорема. Если функция непрерывна на промежутке и интеграл сходится, то сходится и интеграл

Если функция 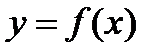непрерывна на промежутке 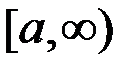и интеграл 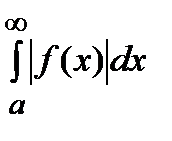сходится, то сходится и интеграл .

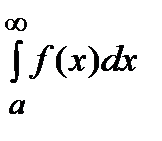Доказательство: Рассмотрим две функци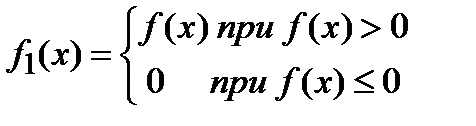и:

и .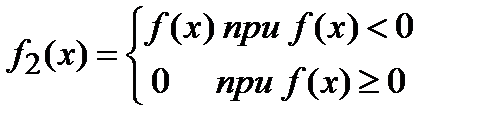

(заметим, что функция 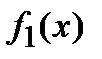совпадает с функцией 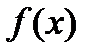в тех точках, где последняя положительна, и равна нулю в остальных точках, а функция 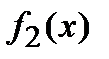совпадает с функцией 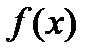в тех точках, где она отрицательна, и равна нулю в остальных точках).

Очевидно, что 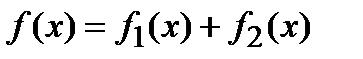. Воспользовавшись теоремой сравнения (в нашем случае 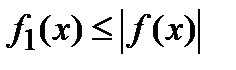и 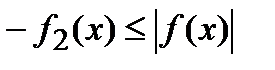), можно утверждать, что интегралы 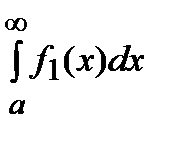и 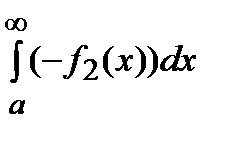, а значит и 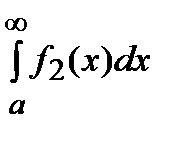сходятся. Но тогда будет сходиться и интеграл 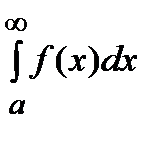, поскольку для него справедливо равенство:

= +

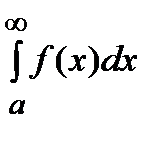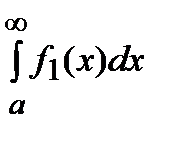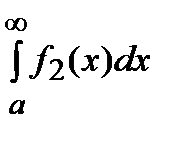
Проверка последнего равенства осуществляется заменой интегралов по бесконечному промежутку соответствующими пределами.

Отметим, что если вместе с интегралом 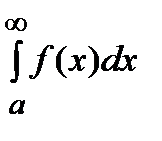сходится и интеграл 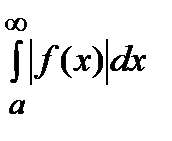, то интеграл 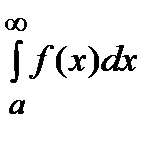называется абсолютно сходящимся, в противном случае (если сходится только интеграл 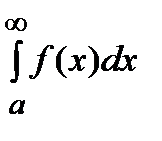) он называется условно сходящимся.

Аналогичные теоремы можно сформулировать как для несобственных интегралов первого рода по промежуткам 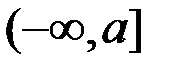и 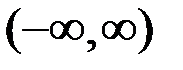, так и для несобственных интегралов второго рода.