Теорема (признак сравнения)

Если на промежутке 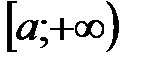непрерывные функци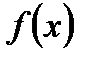и и 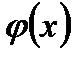удовлетворяют условию 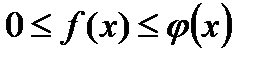для 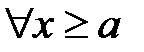, то из сходимости интеграла 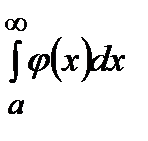следует сходимость интеграла 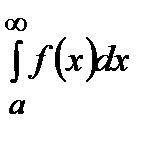, а из расходимости 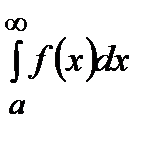следует расходимость .

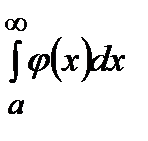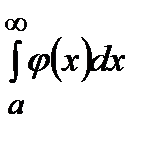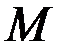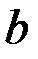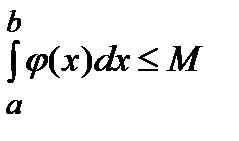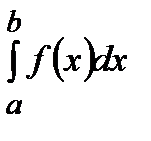
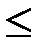
Доказательство. Предположим, что интеграл сходится и равен , тогда для любого будет выполняться неравенство: и, следовательно, будут выполняться неравенства: 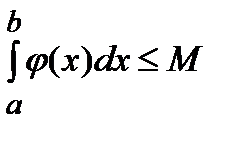. Если теперь на интеграл 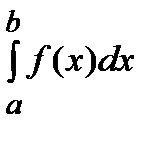смотреть как на функцию от 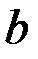, то эта функция будет монотонно возрастающей на бесконечном промежутке 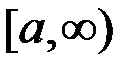и ограниченной на этом промежутке. Следовательно, она имеет конечный предел: 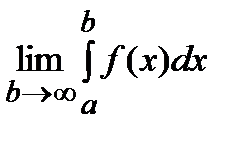, то есть интеграл 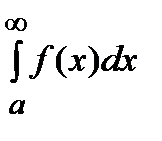сходится.

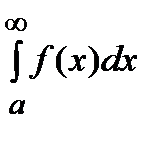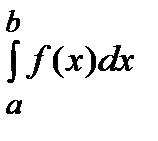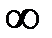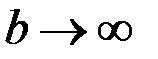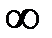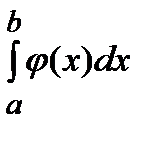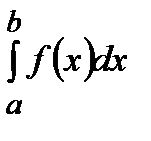
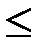
Если теперь интеграл расходится, то возрастающая функция стремится к при . Но тогда, тем более, будет стремиться к и функция , так как 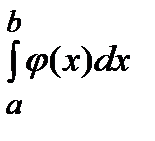. То есть интеграл 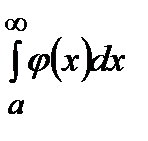будет расходиться.