Теорема (предельный признак сравнения)

Если на промежутке 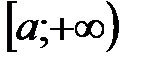функци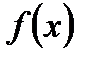и и 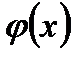непрерывны и неотрицательны, а предел их 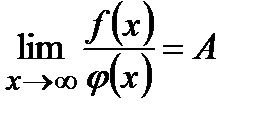, где 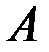- число, не равное нулю, то оба несобственных интеграла 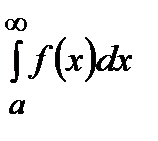и 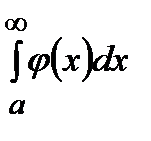либо сходятся, либо расходятся одновременно.

Мы не будем приводить доказательство этой теоремы, а укажем только направление рассуждений для организации доказательства.

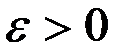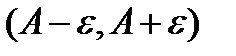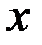Указание. Если выбрать настолько малым, чтобы окрестность не содержала , то для «больших» будет выполняться неравенство 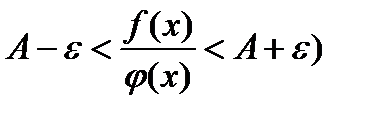, или 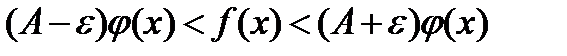и остается воспользоваться первым признаком сравнения.