Квадратная матрица 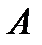 называется обратимой, если существует матрица такая, что
называется обратимой, если существует матрица такая, что 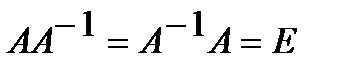 . Эту матрицу называют обратной к матрице
. Эту матрицу называют обратной к матрице 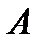 и обозначают
и обозначают 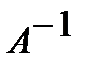 .
.
Каждой квадратной матрице 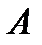 соответствует определитель
соответствует определитель 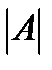 . Оказывается, что если
. Оказывается, что если 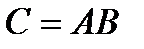 , то
, то 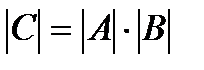 . Так как
. Так как 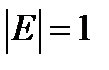 , то
, то 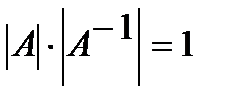 .
.
Необходимым и достаточным условием существования обратной матрицы является условие 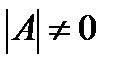 .
.
Алгебраическим дополнением 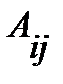 элемента
элемента 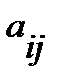 называется произведение числа
называется произведение числа 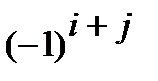 на определитель, получающийся при вычеркиванием
на определитель, получающийся при вычеркиванием 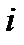 -ой строки и
-ой строки и 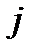 -го столбца. Например, определитель
-го столбца. Например, определитель
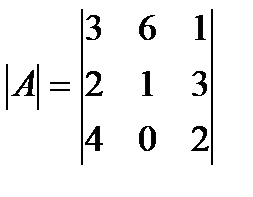
имеет следующие алгебраические дополнения:
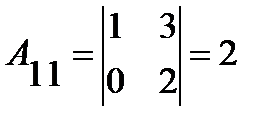 ;
; 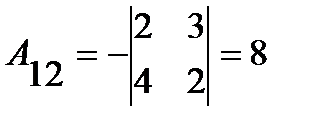 ;
; 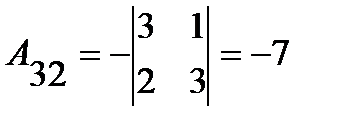 ;
; 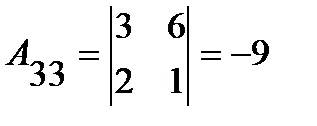 .
.
Если определитель матрицы 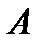 отличен от нуля
отличен от нуля 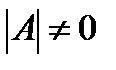 , то обратную матрицу строят следующим образом:
, то обратную матрицу строят следующим образом:
1) находят все алгебраические дополнения;
2) составляют матрицу алгебраических дополнений 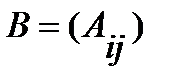 ;
;
3) транспонируют матрицу B и умножают на число 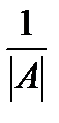 .
.
Полученная матрица 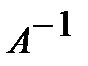 и будет обратной матрицей.
и будет обратной матрицей.
Задача. Решить матричным способом систему уравнений
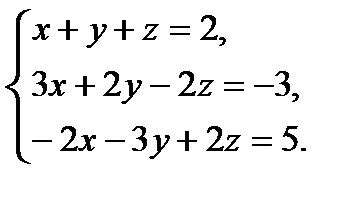
Решение. Положим, что
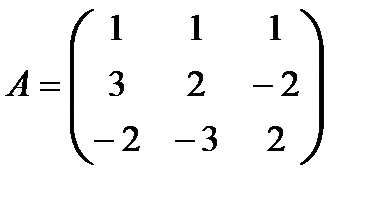 ;
; 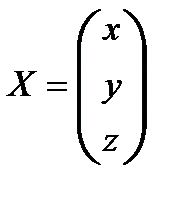 ;
; 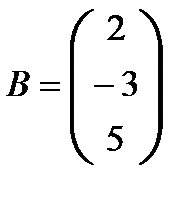 .
.
Тогда матричная запись рассматриваемой системы уравнений будет иметь вид
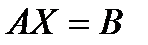 . (10)
. (10)
Найдем определитель 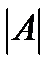 матрицы
матрицы 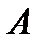 :
:
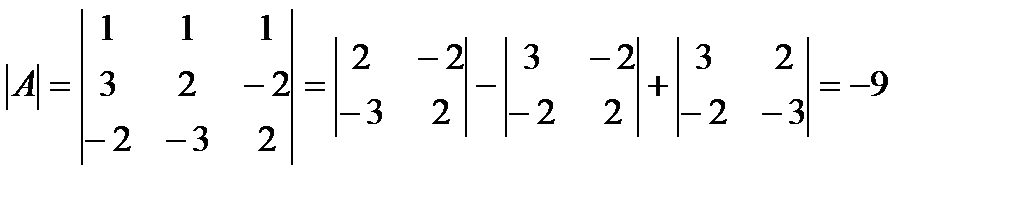 .
.
Так как 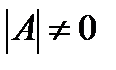 , то существует обратная матрица
, то существует обратная матрица 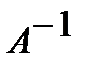 . Умножая слева на матрицу
. Умножая слева на матрицу 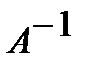 равенство (10), получим, что
равенство (10), получим, что 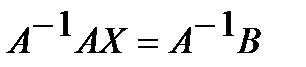 или
или 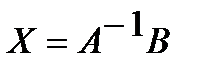 . Найдем обратную матрицу
. Найдем обратную матрицу 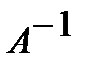 :
:
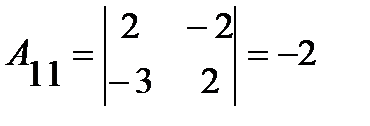 ;
; 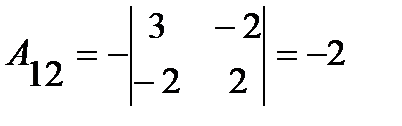 ;
; 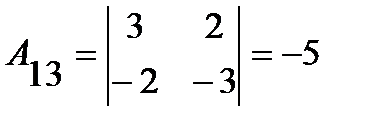 ;
;
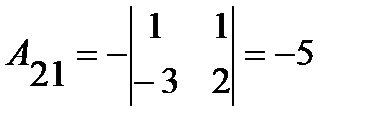 ;
; 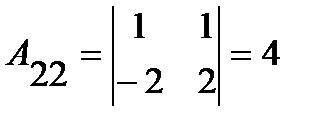 ;
; 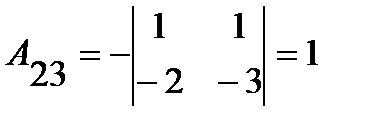 ;
;
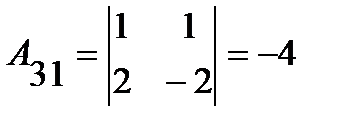 ;
; 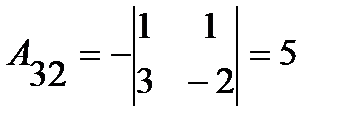 ;
; 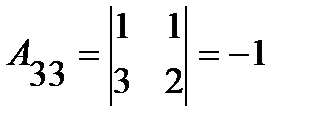 .
.
Обратная матрица 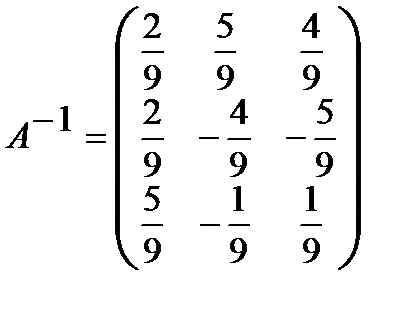 .
.
Но тогда 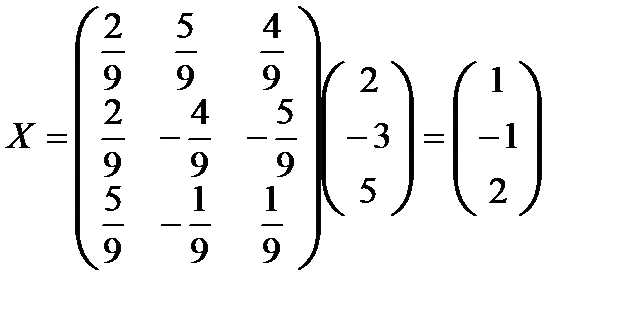 .
.
Ответ: 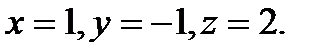
 2015-04-12
2015-04-12 671
671








