Умножение вектора на вектор бывает двух типов: скалярное и векторное. В результате скалярного умножения двух векторов получаем число (скаляр). В результате векторного произведения двух векторов получаем вектор.
Скалярным произведением 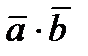 двух ненулевых векторов
двух ненулевых векторов 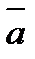 и
и 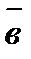 называется число, равное произведению длин этих векторов на косинус угла между ними:
называется число, равное произведению длин этих векторов на косинус угла между ними: 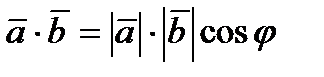 , где
, где 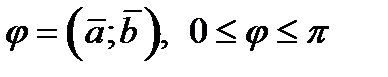 .
.
Свойства скалярного произведения во многом сходны со свойствами произведения действительных чисел.
Векторным произведением двух векторов 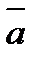 и
и 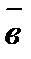 называется вектор
называется вектор 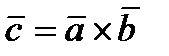 , который:
, который:
1) имеет модуль, численно равный площади параллелограмма, построенного на векторах 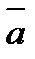 и
и 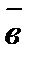 :
: 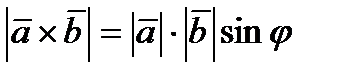 ;
;
2) перпендикулярен к плоскости этого параллелограмма;
3) направлен в такую сторону, с которой кратчайший поворот от 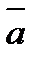 к
к 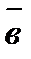 рассматривается совершающимся против часовой стрелки (такое расположение векторов
рассматривается совершающимся против часовой стрелки (такое расположение векторов 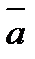 ,
, 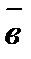 и
и 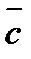 называется правой тройкой векторов).
называется правой тройкой векторов).
Отличительная особенность векторного произведения состоит в том, что для него переместительное свойство (коммутативность) не имеет места. От перестановки векторов – сомножителей векторное произведение изменяет знак на противоположный: 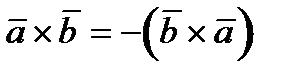 .
.
Три вектора могут быть перемножены несколькими способами. Чаще всего рассматривают смешанное произведение двух векторов векторно и на третий скалярно. В результате получают число.
Смешанное произведение трех векторов 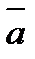 ,
, 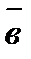 и
и 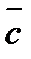 , которое обозначается
, которое обозначается 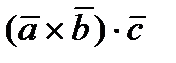 или
или 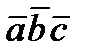 , есть скаляр, абсолютная величина которого равна обьему параллелепипеда, построенного на векторах
, есть скаляр, абсолютная величина которого равна обьему параллелепипеда, построенного на векторах 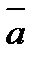 ,
, 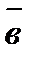 и
и 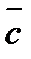 , как на ребрах.
, как на ребрах.
Пусть заданы два вектора 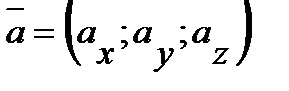 и
и 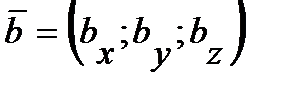 .
.
Скалярное произведение двух ненулевых векторов равно сумме произведений соответствующих координат этих векторов:
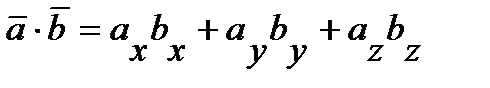 .
.
Угол между векторами вычисляется по формуле
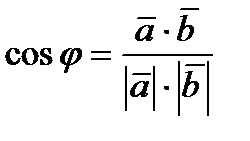 ,
,
или в координатной форме 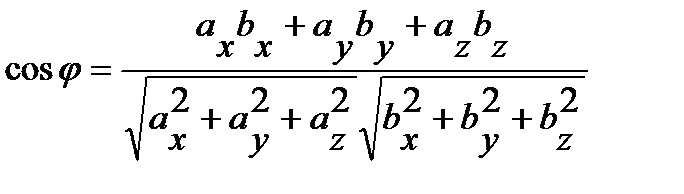 .
.
Условием перпендикулярности ненулевых векторов  и
и  является равенство нулю их скалярного произведения:
является равенство нулю их скалярного произведения:
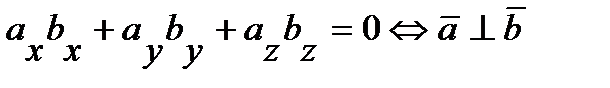 .
.
Векторное произведение ненулевых векторов 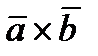 выражается через координаты данных векторов
выражается через координаты данных векторов 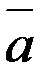 и
и 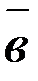 следующим образом:
следующим образом:
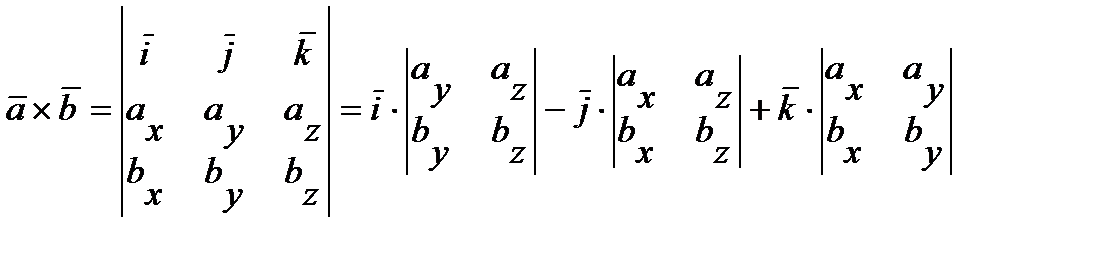 .
.
Равенство нулю векторного произведения двух ненулевых векторов является условием их коллинеарности, т.е. 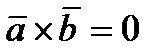
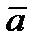 ½½
½½ 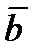 .
.
Скаляр 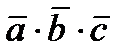 , представляющий смешанное произведение трех векторов, равняется определителю третьего порядка, составленному из координат этих трех векторов:
, представляющий смешанное произведение трех векторов, равняется определителю третьего порядка, составленному из координат этих трех векторов:
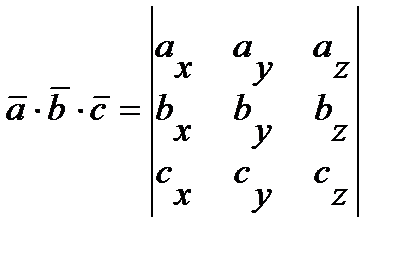 .
.
Равенство нулю смешанного произведения трех ненулевых векторов является условием их компланарности: 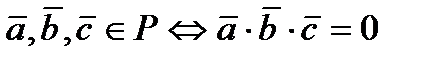 .
.
Задача. Определить внутренние углы 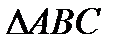 c вершинами
c вершинами 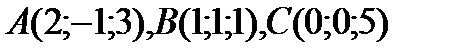 .
.
Решение. Найдем 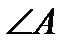 . Для этого надо найти векторы
. Для этого надо найти векторы 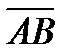 и
и 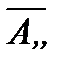 . Зная векторы
. Зная векторы 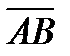 и
и 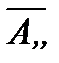 , из формулы (2) получим
, из формулы (2) получим
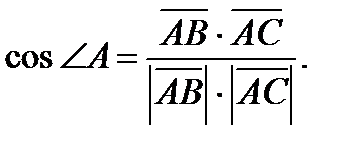
Легко видеть, что 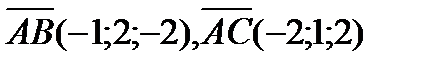 . Тогда
. Тогда
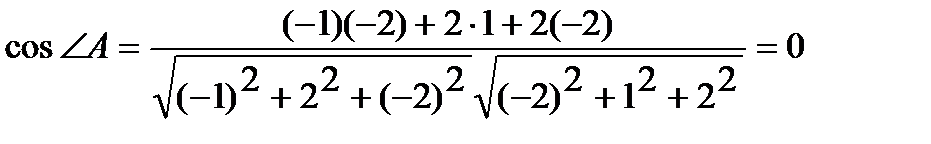 .
.
Отсюда 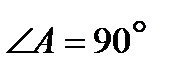 .
.
Аналогично, находя предварительно, что 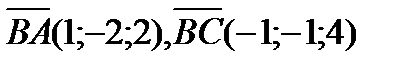 , получим
, получим
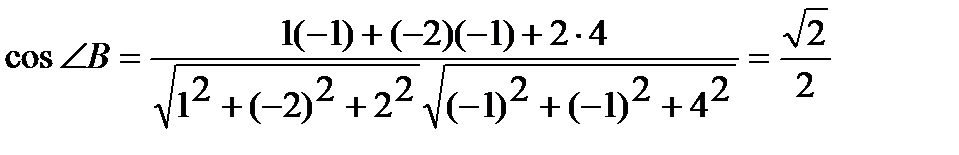 .
.
Отсюда 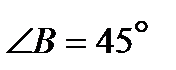 и
и 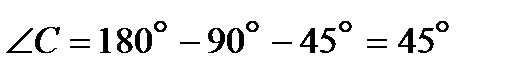 .
.
Задача. Вычислить площадь треугольника с вершинами 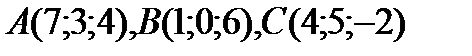 .
.
Решение. Найдем вначале площадь 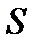 параллелограмма, построенного на векторах
параллелограмма, построенного на векторах 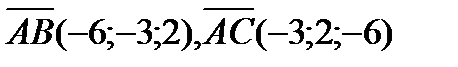 как на сторонах. По определению векторного произведения
как на сторонах. По определению векторного произведения 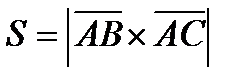 . Но
. Но
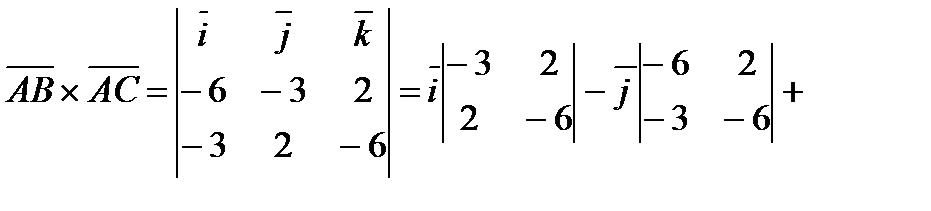
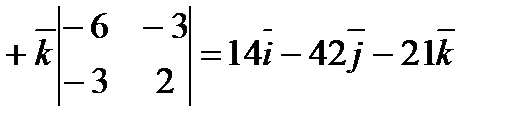 .
.
Тогда 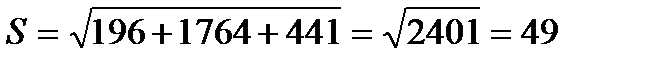 .
.
Следовательно, 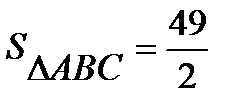 .
.
Задача. Вычислить объем пирамиды с вершинами 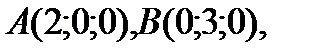
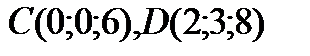 .
.
Решение. Найдем координаты векторов 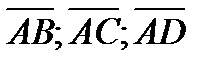 . Очевидно, что
. Очевидно, что 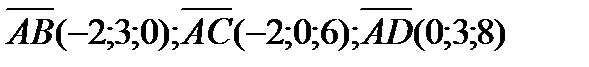 .
.
Тогда 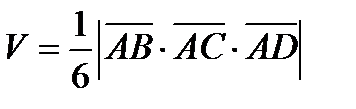 . Но
. Но 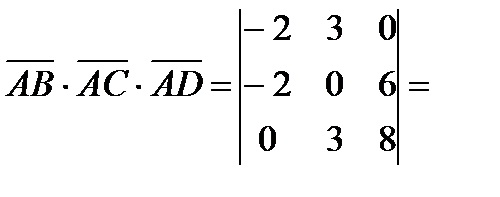
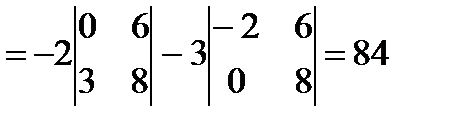 ..
..
Следовательно, 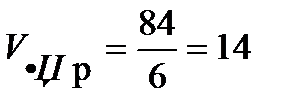 .
.
 2015-04-12
2015-04-12 30086
30086
