Интегрированием по частям называется нахождение интеграла по формуле:
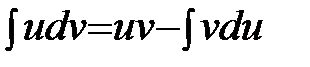 ,
,
где 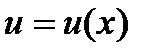
 и
и 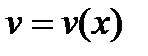 — непрерывно дифференцируемые функции от
— непрерывно дифференцируемые функции от 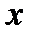 . С помощью этой формулы нахождение интеграла
. С помощью этой формулы нахождение интеграла 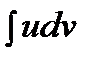 сводится к отысканию другого интеграла
сводится к отысканию другого интеграла 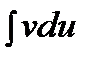 . Ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.
. Ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.
Применяется формула в следующих случаях:
1) Подынтегральная функция является произведением многочлена на показательную или тригонометрическую функцию.
Это интегралы вида: 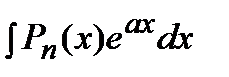 ,
, 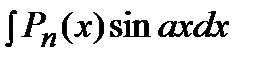 ,
, 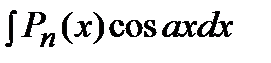 .
.
В этом случае в качестве 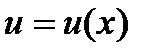 выбирается многочлен
выбирается многочлен 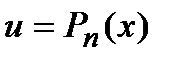 .
.
Пример. 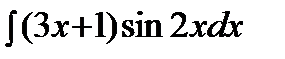 .
.
Решение. Подынтегральная функция есть произведение многочлена на тригонометрическую функцию (1 случай). Поэтому в качестве 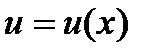 выбирается многочлен.
выбирается многочлен.
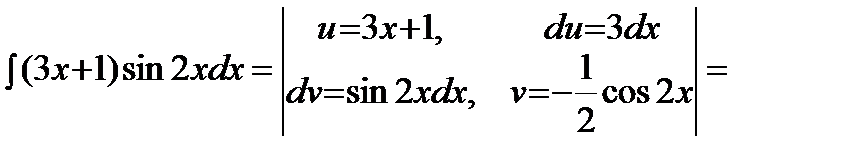
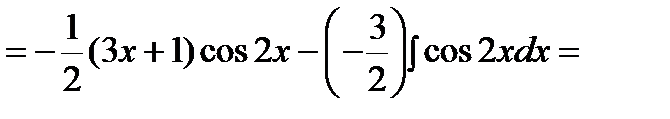
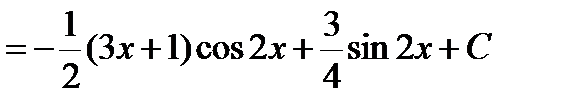 .
.
2) Подынтегральная функция является произведением многочлена на логарифмическую или обратную тригонометрическую функцию.
Это интегралы вида:  ,
, 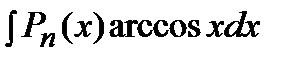 ,
, 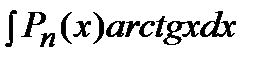 ,
, 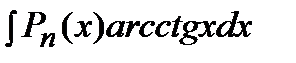 ,
, 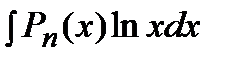 .
.
В качестве 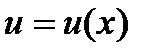 следует принимать обратную тригонометрическую или логарифмическую функцию.
следует принимать обратную тригонометрическую или логарифмическую функцию.
Пример. 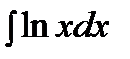 .
.
Решение. Подынтегральная функция есть логарифмическая функция (2 случай). Поэтому в качестве 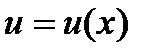 выбирается логарифмическая функция.
выбирается логарифмическая функция.
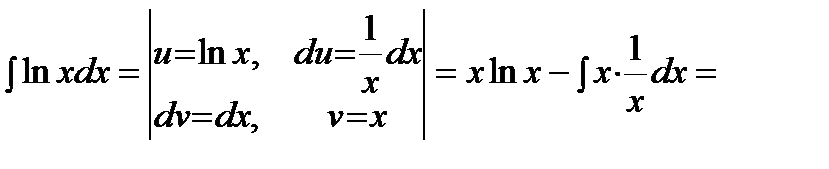
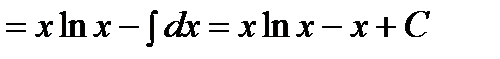 .
.
 2015-04-12
2015-04-12 429
429








