141. Даны векторы: 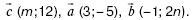 Найдите числа m и n, если
Найдите числа m и n, если 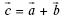 .
.
142. Дан вектор 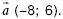 Найдите координаты вектора
Найдите координаты вектора 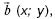 такого
такого
что 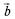 сонаправлен с
сонаправлен с 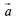 и его длина в два раза больше, чем у вектора
и его длина в два раза больше, чем у вектора 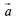 .
.
143. Найдите координаты точки А (х; у), если она симметрична точке В (–20; 11) относительно точки М (0; –5).
144. Найдите координаты точки С (х; у), если она принадлежит оси абсцисс и одинаково удалена от точек А (–14; 5) и В (3; 8).
145. Даны точки М (–2; 6), К (1; 2) и L (4; –2). Определите, принадлежат ли данные точки одной прямой.
146. Определите, будет ли треугольник ОРQ равносторонним, если О – начало координат и Р (5; 6), Q (–6; 5).
147. Найдите сумму векторов: 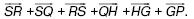
148. Верно ли равенство: 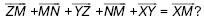
149. В окружности с центром в точке О проведены диаметр АВ и радиус ОС.
Пусть 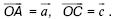 Необходимо выразить векторы
Необходимо выразить векторы 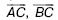 через векторы
через векторы 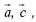 и доказать, что угол АСВ прямой.
и доказать, что угол АСВ прямой.
150. Точка М делит отрезок КL в отношении 2:3. Найдите координаты вектора 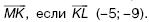
151. Даны векторы 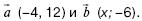 Найдите значение х, при котором данные векторы будут перпендикулярны.
Найдите значение х, при котором данные векторы будут перпендикулярны.
152. Дан треугольник ABС и точка G – точка пересечения его медиан. Докажите, что 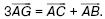
153. Дан параллелограмм АВСD. Докажите, что для любой точки М 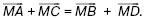
154. На сторонах угла О отложены отрезки ОА = ОВ. Докажите, что вектор 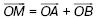 лежит на биссектрисе угла О.
лежит на биссектрисе угла О.
155. В треугольнике АВС точка М – середина стороны ВС. Точка D симметрична точке А относительно точки М. Докажите, что: 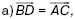
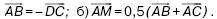
156. Найдите модуль вектора 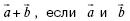 единичные векторы, и угол между ними равен 60°.
единичные векторы, и угол между ними равен 60°.
157. Две равные окружности пересекаются в точках М и N. Через них проведены две параллельные секущие. Первая пересекает окружности в точках А и В, вторая – в точках С и D. Докажите, что: 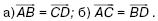
158. Запишите условие того, что четырехугольник АВСD является: а) параллелограммом; б) трапецией.
159. Даны четыре вектора 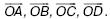 Запишите условие того, что точка О является точкой пересечения диагоналей АС и ВD выпуклого четырехугольника АВСD.
Запишите условие того, что точка О является точкой пересечения диагоналей АС и ВD выпуклого четырехугольника АВСD.
160. В окружность с центром О вписан правильный пятиугольник АВСDЕ. Докажите, что 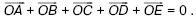
 2015-04-12
2015-04-12 928
928








