Коллинеарными

Если же векторы ,

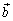
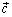, компланарны, то либо один из

них, например 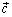, лежит в одной

плоскости с двумя другими неколлинеарными векторами (следовательно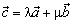

; или 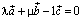), либо все три вектора

коллинеарны (следовательно ).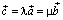

Тем самым следствие полностью доказано.

Следствие: Если три вектора некомпланарны, то они линейно независимы.

Теорема: Любой вектор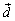

может быть представлен в виде линейной комбинации трех некомпланарных векторов

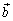, и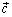

(т.е. найдутся такие числа λ, μ, ν, что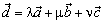

). Такое представление единственно.

Никакие два из векторов ,

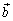
и 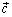не коллинеарны, иначе все три

были бы компланарны. Поэтому, если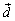

компланарен с какими-нибудь двумя из данных векторов, то наше утверждение