Определение и примеры евклидовых пространств

1. Определение вещественного евклидова пространства. Вещественное линейное пространство R называется вещественным евклидовым пространством (или просто евклидовым пространством), если выполнены следующие два требования.
I. Имеется правило, посредством которого любым двум элементам этого пространства х и у ставится в соответствие вещественное число, называемое скалярным произведением этих элементов и обозначаемое символом (х, у).
П. Указанное правило подчинено следующим четырем аксиомам:
1°. (х, у) = (у, х) (переместительное свойство или симметрия);
2°. (x₁ + x2, у) = (х₁,у) + (х₂, у) (распределительное свойство);
3°. (λх, у) = λ(х, у) для любого вещественного λ;
4°. (х, х) > 0, если х — ненулевой элемент; (х, х) = 0, если х — нулевой элемент.
Подчеркнем, что при введении понятия евклидова пространства мы абстрагируемся не только от природы изучаемых объектов, но и от конкретного вида правил образования суммы элементов, произведения элемента на число и скалярного произведения элементов (важно лишь, чтобы эти правила удовлетворяли восьми аксиомам линейного пространства и четырем аксиомам скалярного произведения).
Если же природа изучаемых объектов и вид перечисленных правил указаны, то евклидово пространство называется конкретным.
Приведем примеры конкретных евклидовых пространств.
Пример 1. Рассмотрим линейное пространство В₃, всех свободных векторов. Скалярное произведение любых двух векторов определим так, как это было сделано в аналитической геометрии (т. е. как произведение длин этих векторов на косинус угла между ними). В курсе аналитической геометрии была доказана справедливость для так определенного скалярного произведения аксиом 1°- 4° (см. выпуск «Аналитическая геометрия», гл.2, §2, п.З). Стало быть, пространство В₃ с так определенным скалярным произведением является евклидовым пространством.
Пример 2. Рассмотрим бесконечномерное линейное пространство С [а, b] всех функций x(t), определенных и непрерывных на сегменте а ≤ t ≤ b. Скалярное произведение двух таких функций x(t) и y(t) определим как интеграл (в пределах от а до b) от произведения этих функций

Элементарно проверяется справедливость для так определенного скалярного произведения аксиом 1°-4°. В самом деле, справедливость аксиомы 1° очевидна; справедливость аксиом 2° и 3° вытекает из линейных свойств определенного интеграла; справедливость аксиомы 4° вытекает из того, что интеграл 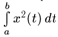от непрерывной неотрицательной функции x²(t) неотрицателен и обращается в нуль лишь тогда, когда эта функция тождественно равна нулю на сегменте а ≤ t ≤ b (см. выпуск «Основы математического анализа», часть I, свойства 1° и 2° из п. 1 §6 гл. 10) (т.е. является нулевым элементом рассматриваемого пространства).
Таким образом, пространство С [а, b] с так определенным скалярным произведением представляет собой бесконечномерное евклидово пространство.
Пример 3. Следующий пример евклидова пространства дает n-мерное линейное пространство А_n упорядоченных совокупностей n вещественных чисел, скалярное произведение двух любых элементов х= (х₁, x₂,...,х_n) и у = (y₁, y₂,...,y_n) которого определяется равенством

(х, у) = x₁y₁ + x₂y₂ +... + x_ny_n. (4.2)

Справедливость для так определенного скалярного произведения аксиомы 1° очевидна; справедливость аксиом 2° и 3° легко проверяется достаточно вспомнить определение операций сложения элементов и умножения их на числа:

(х₁, x₂,...,х_n) + (y₁, y₂,...,y_n) = (x₁+ y₁, x₂ + y₂,...,x_n + y_n),

λ(х₁, x₂,...,х_n) = (λх₁, λx₂,..., λх_n);

наконец, справедливость аксиомы 4° вытекает из того, что (х, х) = х₁² + x₂²+...+ х_n² всегда является неотрицательным числом и обращается в нуль лишь при условии х₁ = х₂ =... = х_n = 0.
Рассмотренное в этом примере евклидово пространство часто обозначают символом Е_n.