Аффинная система координат

Введем в множествах Eⁿ и Vⁿ дополнительную структуру (*):

1) В Eⁿ зафиксируем произвольную точку O;

2) В пространстве Vⁿ зафиксируем базис e ₁, e ₂, …, e_n.

То есть мы фиксировали упорядоченную пару (O, ).

Каждой точке A Î Eⁿ однозначно сопоставляется радиус-вектор 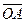= 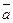, 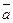Î Vⁿ.

Для вектора 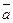Î Vⁿ однозначно определяется набор (x ₁, x ₂, …, x_n) Î Rⁿ - координаты вектора 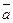в базисе e ₁, e ₂, …, e_n, то есть 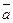= x ₁ e ₁ + x ₂ e ₂ +… x_ne_n.

Пусть = 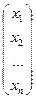, = (e ₁ e ₂ … e_n), тогда = .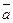

Определим отображение w: Eⁿ ® Rⁿ по следующей формуле: w(A) = .

Определение. Отображение w будем назвать аффинной системой координат в Eⁿ.

Определение. Упорядоченный набор Î Rⁿ такой, что w(A) = будем назвать аффинными координатами точки A в системе координат w.

Определение. Фиксированную точку O будем называть началом координат.

Теорема. Аффинная система координат - это биективное отображение.

Доказательство ( провестисамостоятельно ).

Обозначение: вместо записи w(A) = мы будем употреблять более распространенную запись A(x₁, x₂, …, x_n).