Уравнение плоскости по точке и нормальному вектору

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ

Поверхности и линии в пространстве

Определение 1. Уравнением поверхности (в фиксированной системе координат) называется такое уравнение с тремя переменными 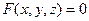, которому удовлетворяют координаты 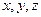любой точки данной поверхности и только они.

Здесь 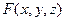– некоторая зависимость между переменными .

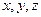Пример 1. 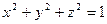– уравнение сферы ().

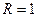Определение 2. Линию в пространстве можно рассматривать как пересечение двух поверхностей, поэтому она определяется двумя уравнениями:

.

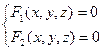Пример 2. .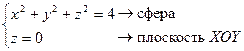

Линия, как пересечение поверхностей, определяет окружность, лежащую в плоскости ().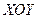

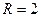Уравнение плоскости по точке и нормальному вектору

Дано: 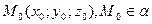, 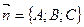– нормальный вектор, .

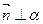Написать уравнение плоскости.

Выберем произвольную точку ,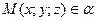

тогда 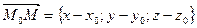, , 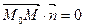т.е.

(1)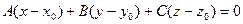

– уравнение плоскости.