Даны координаты вершин треугольника 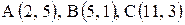 .
.
1) Вычислить длину стороны 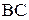 .
.
2) Составить уравнение линии 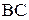 .
.
3) Составить уравнение высоты, проведенной из вершины А, и найти ее длину.
4) Найти точку пересечения медиан.
5) Найти косинус внутреннего угла при вершине В.
6) Найти координаты точки М, расположенной симметрично точке А, относительно прямой ВС.
 А
А
О
В С
М
Решение
1. Длина стороны ВС равна модулю вектора 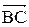 .
.
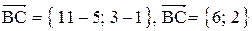 ;
; 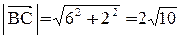 .
.
2. Уравнение прямой ВС: 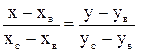 ;
; 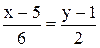 ;
; 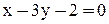 .
.
3. Уравнение высоты АК запишем как уравнение прямой, проходящей через точку 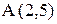 перпендикулярно вектору
перпендикулярно вектору 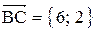 :
: 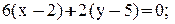
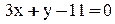 . Длину высоты АК можно найти как расстояние от точки А до прямой ВС:
. Длину высоты АК можно найти как расстояние от точки А до прямой ВС: 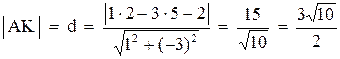 .
.
4. Найдем координаты точки N – середины стороны ВС:
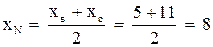 ;
; 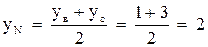 ;
; 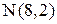 .
.
Точка пересечения медиан О делит каждую медиану на отрезки в отношении 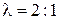 .
.
Используем формулы деления отрезка в данном отношении 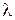 :
:
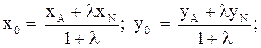
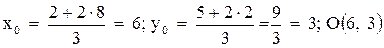 .
.
5. Косинус угла при вершине В найдем как косинус угла между векторами 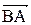 и
и 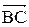
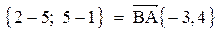 ;
; 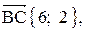
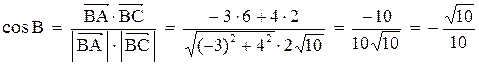 .
.
6. Точка М, симметричная точке А относительно прямой ВС, расположена на прямой АК, перпендикулярной к прямой ВС, на таком же расстоянии от прямой, как и точка А. Координаты точки К найдем как решения системы 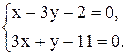 Систему решим по формулам Крамера:
Систему решим по формулам Крамера: 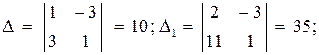
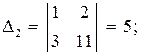
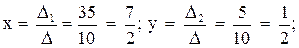
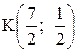 .
.
Точка К является серединой отрезка АМ.
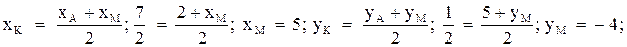
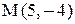 .
.
Контрольные варианты к задаче 2
Даны координаты вершин треугольника АВС. Требуется:
1) вычислить длину стороны ВС;
2) составить уравнение линии ВС;
3) составить уравнение высоты, проведенной из вершины А;
4) вычислить длину высоты, проведенной из вершины А;
5) найти точку пересечения медиан;
6) вычислить внутренний угол при вершине В;
7) найти координаты точки М, расположенной симметрично точке А относительно прямой ВС.
| 1. | 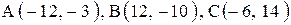 . . | 2. | 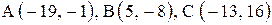 . . |
| 3. | 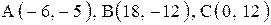 . . | 4. | 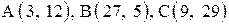 . . |
| 5. | 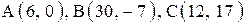 . . | 6. | 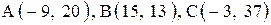 . . |
| 7. | 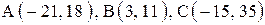 . . | 8. | 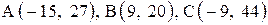 . . |
| 9. | 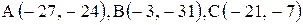 . . | 10. | 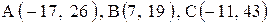 . . |
| 11. | 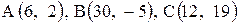 . . | 12. | 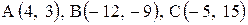 . . |
| 13. | 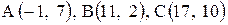 . . | 14. | 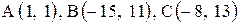 . . |
| 15. | 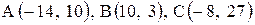 . . | 16. | 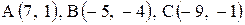 . . |
| 17. | 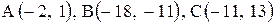 . . | 18. | 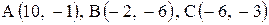 . . |
| 19. | 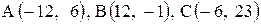 . . | 20. | 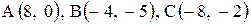 . . |
| 21. | 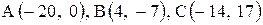 . . | 22. | 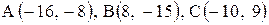 . . |
| 23. | 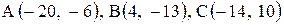 . . | 24. | 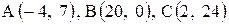 . . |
| 25. | 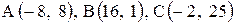 . . | 26. | 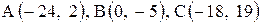 . . |
| 27. | 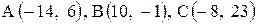 . . | 28. | 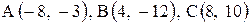 . . |
| 29. | 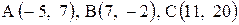 . . | 30. | 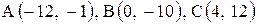 . . |
 2015-04-12
2015-04-12 15094
15094
