Уравнение плоскости, проходящей через три точки, не принадлежащие одной прямой

Даны три точки, не лежащие на одной прямой: 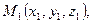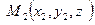, 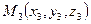. Пусть 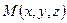– произвольная точка пространства.

Точка 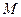принадлежит плоскости (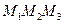) тогда и только тогда, когда векторы 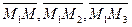компланарны.

Условие компланарности трех векторов – это равенство нулю их смешанного произведения:

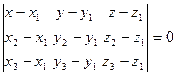. (7)

Уравнение (7) – это уравнение плоскости, проходящей через три заданные точки