2015-04-12
878
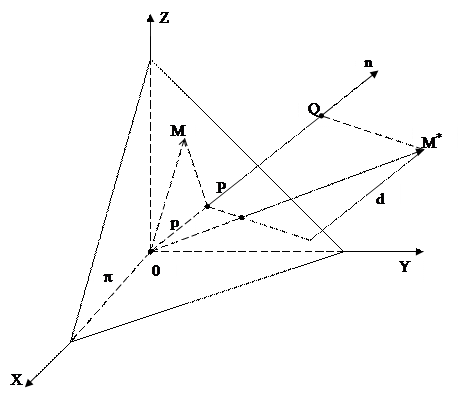
Пусть существует плоскость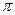 
. Проведем нормаль 
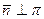через начало координат О. Пусть заданы 
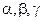– углы, образованные нормалью 
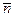с осями координат. 
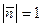. Пусть 
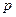– длина отрезка нормали 
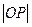до пересечения с плоскостью. Считая известными направляющие косинусы нормали 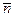, выведем уравнение плоскости .
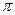Пусть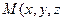 
) – произвольная точка плоскости. Вектор единичной нормали имеет координаты 
. Найдем проекцию вектора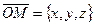 
на нормаль.
.
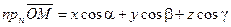Поскольку точка М принадлежит плоскости, то
.
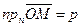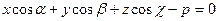(8)
Это и есть уравнение заданной плоскости, называющееся нормальным.
