Пусть дана плоскость 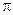 , М *
, М * 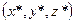 – точка пространства, d – её расстояние от плоскости.
– точка пространства, d – её расстояние от плоскости.
Определение. Отклонением точки М* от плоскости называется число (+d), если M* лежит по ту сторону от плоскости, куда указывает положительное направление нормали 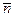 , и число (- d), если точка расположена по другую сторону плоскости:
, и число (- d), если точка расположена по другую сторону плоскости:
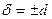 .
.
Теорема. Пусть плоскость 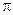 с единичной нормалью
с единичной нормалью  задана нормальным уравнением:
задана нормальным уравнением:
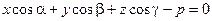 .
.
Пусть М * 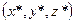 – точка пространства Отклонение т. M * от плоскости задаётся выражением
– точка пространства Отклонение т. M * от плоскости задаётся выражением
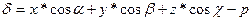 . (9)
. (9)
Доказательство. Проекцию т. 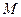 * на нормаль обозначим Q. Отклонение точки М* от плоскости равно
* на нормаль обозначим Q. Отклонение точки М* от плоскости равно
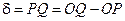 .
.
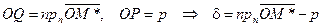 ;
;
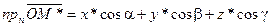 ;
;
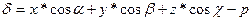 (9)
(9)
Правило. Чтобы найти отклонение т. M * от плоскости, нужно в нормальное уравнение плоскости подставить координаты т. M*. Расстояние от точки до плоскости равно 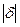 .
.
 2015-04-12
2015-04-12 678
678








