Канонические уравнения прямой в пространстве

Пусть 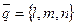– направляющий вектор прямой L, а 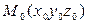– точка, принадлежащая прямой. Пусть 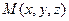– точка с переменными координатами.

Чтобы точка 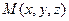принадлежала прямой L, вектор 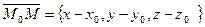должен быть коллинеарным вектору :

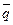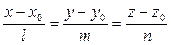. (2)

Уравнения (2) – это канонические уравнения прямой в пространстве. Пусть прямая L задана общим уравнением:

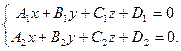
Найти канонические уравнения прямой L.

1). Найдем точку 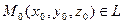. Для этого нужно задать одну из координат, а две другие определить из решения системы (1).

2). Найдем направляющий вектор прямо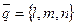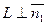й .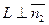

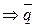
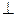
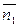и и .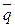

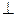
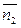
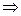
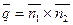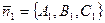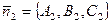
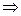, по определению векторного произведения

.

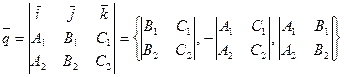Зная координаты точки, принадлежащей прямой, и координаты ее направляющего вектора, можно составить канонические уравнения прямой в виде (2).