Пусть заданы плоскость  : Ax + By + Cz + D = 0
: Ax + By + Cz + D = 0
и прямая L: 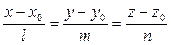 .
.
Пусть 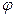 - угол между нормалью к плоскости
- угол между нормалью к плоскости 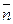 1=
1= 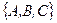 и направляющим вектором прямой
и направляющим вектором прямой 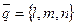 . Тогда угол
. Тогда угол 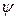 между плоскостью
между плоскостью  и прямой L - дополнительный к этому углу:
и прямой L - дополнительный к этому углу: 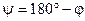 . Тогда
. Тогда
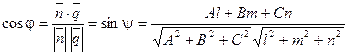 . (6)
. (6)
1). Условие параллельности прямой и плоскости: 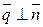
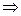
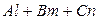 =0
=0
2). Условие перпендикулярности прямой и плоскости: 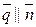
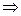
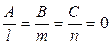
3). Условие принадлежности прямой плоскости. Пусть 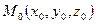 – любая точка прямой. Чтобы прямая лежала в плоскости должны выполняться два условия:
– любая точка прямой. Чтобы прямая лежала в плоскости должны выполняться два условия:
а) направляющий вектор прямой должен быть перпендикулярен нормали к плоскости:
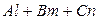 =0,
=0,
б) произвольная точка прямой должна лежать в плоскости:
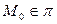
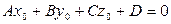 .
.
 2015-04-12
2015-04-12 749
749








