Задача 1. Найти уравнение плоскости  , проходящей через точку
, проходящей через точку 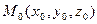 и перпендикулярной заданной прямой
и перпендикулярной заданной прямой 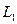 :
: 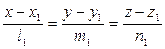 .
.
Кратко:  -?:
-?: 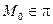 ,
, 
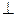
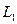 .
.
Решение.
Т.к. 
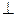
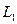 , то нормалью к плоскости можно считать направляющий вектор прямой:
, то нормалью к плоскости можно считать направляющий вектор прямой: 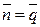 =
= 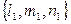 . Воспользуемся уравнением плоскости, проходящей через заданную точку.
. Воспользуемся уравнением плоскости, проходящей через заданную точку.
 :
:  .
.
Задача 2. Найти уравнение плоскости  , проходящей через заданную прямую
, проходящей через заданную прямую 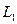 :
: 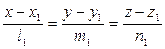 и точку
и точку 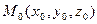
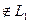 .
.
Кратко.  -?:
-?: 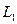
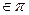 ,
, 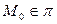 .
.
По условию задачи нам известны две точки, лежащие в плоскости: 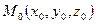 ,
, 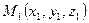 , и вектор
, и вектор 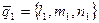 , параллельный плоскости. Произвольная точка
, параллельный плоскости. Произвольная точка 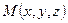 будет принадлежать плоскости, если векторы
будет принадлежать плоскости, если векторы 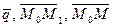 будут компланарны:
будут компланарны:
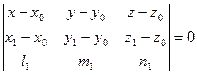 .
.
Это и есть уравнение искомой плоскости. Раскрыв определитель, можно получить общее уравнение плоскости.
Задача 3. Построить плоскость  , проходящую через две заданные параллельные прямые
, проходящую через две заданные параллельные прямые 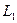 :
: 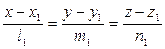 и
и 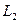 :
: 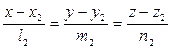 .
.
 -?:
-?: 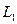
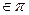 ,
, 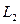
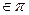 ,
, 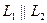 .
.
Эта задача может решаться аналогично предыдущей. Известны две точки 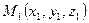 и
и 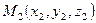 , лежащие в плоскости, и вектор (
, лежащие в плоскости, и вектор (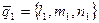 или
или 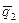 ), параллельный плоскости. Произвольная точка
), параллельный плоскости. Произвольная точка 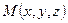 будет принадлежать плоскости, если выполняется условие компланарности трех векторов:
будет принадлежать плоскости, если выполняется условие компланарности трех векторов:
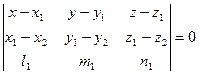 – это уравнение искомой плоскости.
– это уравнение искомой плоскости.
Аналогично решается задача построения плоскости  , проходящей через две пересекающиеся прямые.
, проходящей через две пересекающиеся прямые.
Задача 4. Найти уравнение прямой 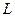 , проходящей через заданную точку
, проходящей через заданную точку 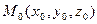 и перпендикулярной плоскости
и перпендикулярной плоскости  :
: 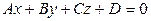
Решение. Так как прямая L перпендикулярна плоскости 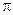 , то ее направляющий вектор параллелен нормали к плоскости. Следовательно, нормаль к плоскости
, то ее направляющий вектор параллелен нормали к плоскости. Следовательно, нормаль к плоскости  может служить направляющим вектором прямой L. Запишем каноническое уравнение прямой:
может служить направляющим вектором прямой L. Запишем каноническое уравнение прямой:
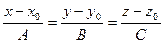 .
.
Задача 5. Построить прямую 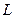 , перпендикулярную двум скрещивающимся прямым.
, перпендикулярную двум скрещивающимся прямым.
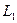 :
: 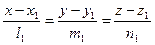 и
и 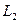 :
:  ,
,
и проходящую через заданную точку 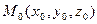 .
.
Решение. Так как прямая L перпендикулярна к прямым L 1 и L 2, то ее направляющий вектор  можно найти как векторное произведение направляющих векторов этих прямых:
можно найти как векторное произведение направляющих векторов этих прямых:
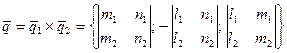 .
.
Тогда можно составить каноническое уравнение искомой прямой:
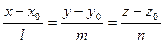 .
.
Задача 6. Найти точку пересечения прямой 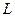 :
: 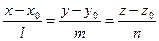 и плоскости
и плоскости 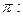
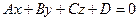 .
.
Решение. Чтобы найти точку пересечения прямой и плоскости, нужно решить совместно уравнения прямой 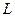 и плоскости
и плоскости 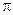 :
:
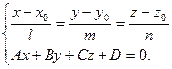
Для этого приведем уравнение прямой к параметрическому виду:
 (*)
(*)
и подставим выражения 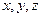 в уравнение плоскости.
в уравнение плоскости.
Решим полученное уравнение с одной неизвестной t, а найденное значение подставим в (*). Полученные значения 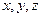 будут координатами искомой точки пересечения.
будут координатами искомой точки пересечения.
Задача 7. Через точку 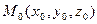 провести прямую, перпендикулярную заданной прямой
провести прямую, перпендикулярную заданной прямой 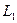 :
: 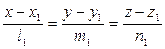 .
.
Решение.
1). Сначала через точку 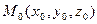 проведем плоскость
проведем плоскость  , перпендикулярную прямой
, перпендикулярную прямой 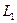 :
:
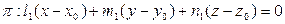 .
.
2). Найдем точку пересечения прямой 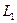 и плоскости
и плоскости  :
: 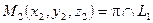 . Для этого решим систему уравнений прямой и плоскости:
. Для этого решим систему уравнений прямой и плоскости:


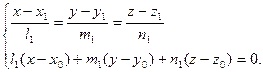
3). Через две точки 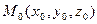 и
и 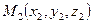 проведем прямую L:
проведем прямую L: 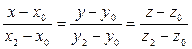 .
.
Задача 8. Найти проекцию точки 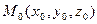 на плоскость
на плоскость  :
: 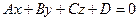 .
.
Решение.
а) Найдем прямую 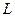 , проходящую через точку
, проходящую через точку 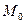 и перпендикулярную плоскости
и перпендикулярную плоскости  :
:
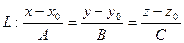 .
.
б) Найдем точку пересечения прямой L и плоскости  :
: 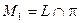 (см. задачу 6).
(см. задачу 6).
Точка М 1 – это искомая проекция.
Задача 9. Найти проекцию точки 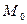 на прямую
на прямую 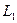 :
: 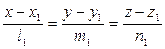 .
.
Решение.
а) Проводим плоскость  :
: 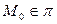 ,
, 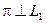 .
.
 :
:  .
.
б) 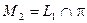 – это искомая проекция.
– это искомая проекция.
Задача 10. Найти проекцию прямой 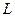 :
: 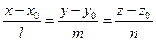 на плоскость
на плоскость 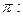
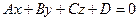 .
.
а) Через прямую проводим плоскость 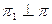 :
: 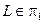 . Используем условие компланарности трех векторов:
. Используем условие компланарности трех векторов: 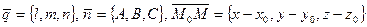 .
.
После преобразований получим общее уравнение плоскости 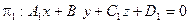 .
.
б) Искомая прямая 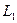 задается пересечением двух плоскостей:
задается пересечением двух плоскостей:  и
и 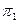 :
: 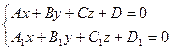
Осталось привести уравнение к каноничному виду.
Задача 11. Найти расстояние от точки 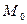 до прямой
до прямой 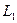 .
.
а) Найти точку 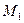 – проекцию точки
– проекцию точки 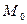 на прямую
на прямую 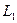 .
.
б) Длина вектора 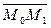 – это искомое расстояние.
– это искомое расстояние.
Задача 12. Найти расстояние между двумя скрещивающимися прямыми 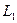 и
и 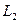 .
.
а) Через прямую 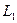 проводим плоскость
проводим плоскость 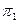 :
: 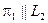 .
.
б) Находим расстояние от любой точки 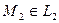 до
до 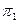 .
.
 2015-04-12
2015-04-12 1418
1418








