Задачи на отметку «5». 1. К прямой а проведены перпендикулярные прямые АС и ВD, причём АС = ВD

1. К прямой а проведены перпендикулярные прямые АС и ВD, причём АС = ВD. Точки С и D принадлежат прямой а. Докажите, что АDВ =

ВDС.

2. По одну сторону от прямой АВ отмечены точки С и D так, что угол САВ равен углу DВА и DВ = СА. Докажите равенство треугольников АDВ и ВСА.

3. Точки D и D₁ являются серединами В В₁

соответствующих сторон равных

треугольников АВС и А₁В₁С₁.

Докажите, что АВD = А₁В₁D₁, С

если угол АСВ равен углуА₁С₁В₁. А D А₁ D₁ С₁

4. Треугольник TSR – равнобедренный с основанием ТR.

а) Докажите, что угол SТР равен уголу RQ;

б) Определите градусную меру угла SТР, если угол SRТ = 46⁰;

в) Определите градусную меру углов SТR и SRТ, если угол SRQ = 134⁰.

S В

А С

Р Т R Q М К

5. Треугольники АВD и DВС – равнобедренные D

с равными основаниями АD и СD. Докажите, что:

а) АВD = СВD;

б) медианы ВМ и ВК этих треугольников равны.

6. Внутри равнобедренного треугольника АВС с основанием АС отмечена точка О так, что АО = ВО = СО. Прямая ВО пересекает сторону АС в точке D. а) Докажите, что отрезок ВD является медианой, биссектрисой и высотой данного треугольника. б) Определите угол ВАО и угол ВСО, если угол АВС = 80⁰.

7. Даны две окружности с общим центром в точке О, АС и ВD – диаметры этих окружностей. Докажите, что треугольники АВО и СDО равны.

8. Отрезки АВ и СD являются диаметрами

О

окружности с центром в точке О. В С

Докажите, что хорды АС и В D равны. А

9. В треугольнике АВС угол А = 38⁰, угол В = 110⁰, D

угол С = 32⁰. На стороне АС отмечены точки D и Е так,

что точка D лежит на отрезке АЕ, ВD = DА, ВЕ = ЕС. М

Найдите угол DВЕ. В F

10. На рисунке АМ = МС, АЕ = DС, угол ВDА равен углу FЕС.

Докажите, что АВ = FС. А D E С

Вопросы к зачету №3.

1.Дайте определение параллельных прямых. Какие два отрезка называются параллельными?

2.Что такое секущая? Назовите пары углов, которые образуются при пересечении двух прямых секущей.

3.Докажите, что если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

4.Докажите, что если при пересечении двух прямых секущей соответственные углы равны, то прямые па­раллельны.

5.Докажите, что если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.

6.Расскажите о практических способах проведения па­раллельных прямых.

7.Объясните, какие утверждения называются аксиома­ми. Приведите примеры аксиом.

8.Докажите, что через данную точку, не лежащую на данной прямой, проходит прямая, параллельная данной.

9.Сформулируйте аксиому параллельных прямых.

10.Какое утверждение называется следствием? Докажи­те, что прямая, пересекающая одну из двух парал­лельных прямых, пересекает и другую.

11.Докажите, что если две прямые параллельны третьей прямой, то они параллельны.

12.Какая теорема называется обратной данной теореме?

Приведите примеры теорем, обратных данным.

13.Докажите, что при пересечении двух параллельных прямых секущей накрест лежащие углы равны.

14.Докажите, что если прямая перпендикулярна к од­ной из двух параллельных прямых, то она перпенди­кулярна и к другой.

15.Докажите, что при пересечении двух параллельных прямых секущей: а) соответственные углы равны; б) сумма односторонних углов равна 180°.

Вопросы к зачету № 4

1.Сформулируйте и докажите теорему о сумме углов треугольника.

2.Какой угол называется внешним углом треугольни­ка? Докажите, что внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

3.Докажите, что в любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.

4.Какой треугольник называют остроугольным? Какой треугольник называется тупоугольным?

5.Какой треугольник называется прямоугольным? Как называются стороны прямоугольного треугольника?

6.Докажите, что в треугольнике:

1)против большей стороны лежит больший угол;

2)обратно, против большего угла лежит большая сто­рона

7. Докажите, что в прямоугольном треугольнике гипо­тенуза больше катета.

8. Докажите, что если два угла треугольника равны, то треугольник равнобедренный.

9.Докажите, что каждая сторона треугольника мень­ше суммы двух других сторон. Что такое неравенство треугольника?

10.Докажите, что сумма двух острых углов прямоуголь­ного треугольника равна 90°.

11.Докажите, что катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипоте­нузы. Сформулируйте и докажите обратное утверж­дение.

12.Сформулируйте и докажите признак равенства ·пря­моугольных треугольников по гипотенузе и острому углу.

13.Сформулируйте и докажите признак равенства пря­моугольных треугольников по гипотенузе и катету.

14.Объясните, какой отрезок называется наклонной, проведенной из данной точки к данной прямой.

15.Докажите, что перпендикуляр, проведенный из точ­ки к прямой, меньше любой наклонной, проведен­ной из этой же точки к этой прямой.

16.Что называется расстоянием от точки до прямой?

17.Докажите, что все точки каждой из двух параллель­ных прямых равноудалены от другой прямой.

18.Что называется расстоянием между двумя парал­лельными прямыми?

19. Объясните, как построить треугольник:

а) по двум сторонам и углу между ними;

б) по стороне и двум прилежащим к ней углам.

20.Объясните, как построить треугольник по трем сто­ронам. Всегда ли эта задача имеет решение?

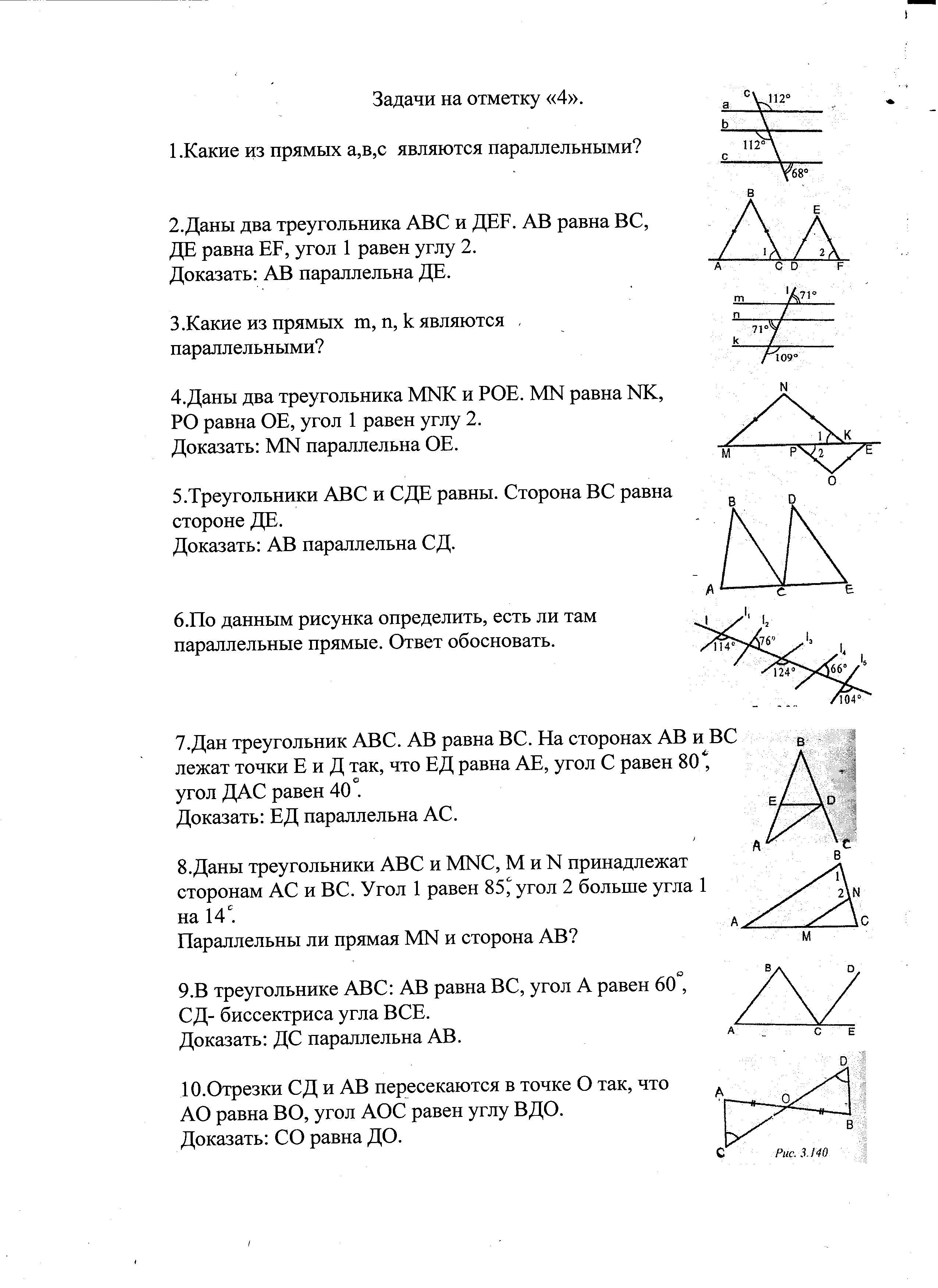
Задачи на отметку «5»

1.Треугольник АВС- равнобедренный с основанием АВ. Биссектрисы углов при основании пересекаются в точке Д. ^ АДВ равен 100.Найти:/.С.

2.Один из углов треугольника равен сумме двух других. Доказать, что данный треугольник- прямоугольный.

З.В треугольнике АВС угол С равен 90, угол В равен 35,СД-высота. Найти: углы треугольника АСД.

4.Найти углы треугольника АВС, если угол А на 60 меньше угла В и в 2 раза меньше угла С.

5.В треугольнике АВС угол С равен 90', угол В равен 70. На катете АС отложен отрезок СД, равный СВ. Найти: углы треугольника АВД.

б.Угол между биссектрисой и высотой, проведенными из вершины наибольшего угла прямоугольного треугольника, равен 14°. Найти: острые углы данного треугольника.

7.Доказать, что основание равнобедренного треугольника параллельно биссектрисе одного из внешних углов.

8.Доказать, что если биссектрисы двух углов треугольника образуют при пересечении угол 135, то этот треугольник- прямоугольный.

9.В прямоугольном треугольнике АВС (угол С прямой) проведена высота С Д. Гипотенуза равна 12см, а угол СВА равен 30\

10.В равнобедренном треугольнике АВС (АВ равно ВС) от вершин при основании отложены равные отрезки АД равно СЕ. Определить углы треугольника ДБЕ, если угол ВЕС равен ПО.

Задачи на отметку «4»

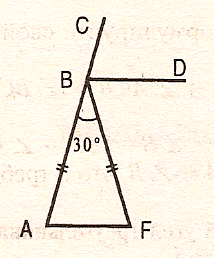
1.АF параллельна ВД, АВ равен ВF, угол В равен 30°

Доказать: ВД- биссектриса угла СВF

Найти: угол А, угол F, сумму углов треугольника АВF

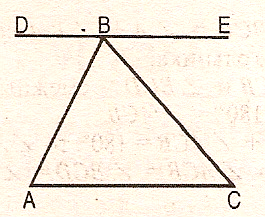
2.Дан треугольник АВС. Через вершину В проведена прямая ДЕ,

параллельная стороне АС.

Найти сумму углов треугольника АВС.

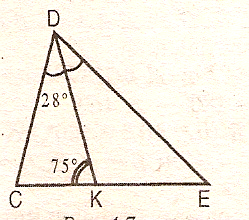
3.ДК- биссектриса СДЕ. Угол СДК равен 28°,угол СКД равен 75°.

Найти: углы треугольника СДЕ.

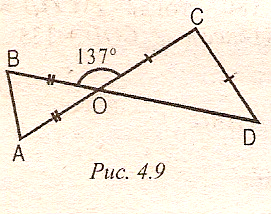4.Прямая АС пересекается с прямой ВД в точке О.ОВ равна ОА,

ОС равна СД, угол ВОС равен 137°.

Найти: углы треугольников АОВ и СДО.

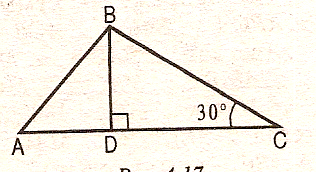5. ВД- высота АВС. ВД равна ДА. Угол С равен 30°.

Найти: угол АВС.

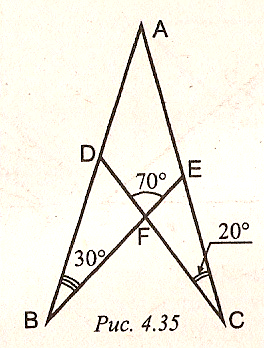6.Дано: угол В равен 30°,угол С равен 20°, угол ДFЕ

равен 70°.Найти: угол А.

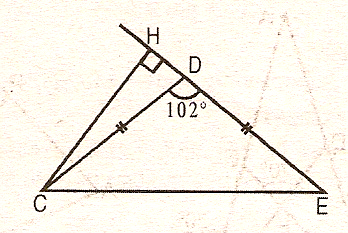
7. В равнобедренном СДЕ с основанием СЕ и углом Д,

равным 102°, проведена высота СH.

Найти: угол ДСH.

8. Внешний угол треугольника равен 140°, а внутренние углы,

не смежные с ним, относятся как 3:4.

Найти: внутренние углы треугольника.

9. Треугольник АВС- равнобедренный с основанием АВ.

Биссектрисы углов при основании пересекаются в точке Д.

Угол АДВ равен 100°. Найти: угол С

10.Один из внутренних углов треугольника в 3 раза больше другого,

а внешний угол, смежный с третьим внутренним углом, равен 100°.

Найти: внутренние углы треугольника

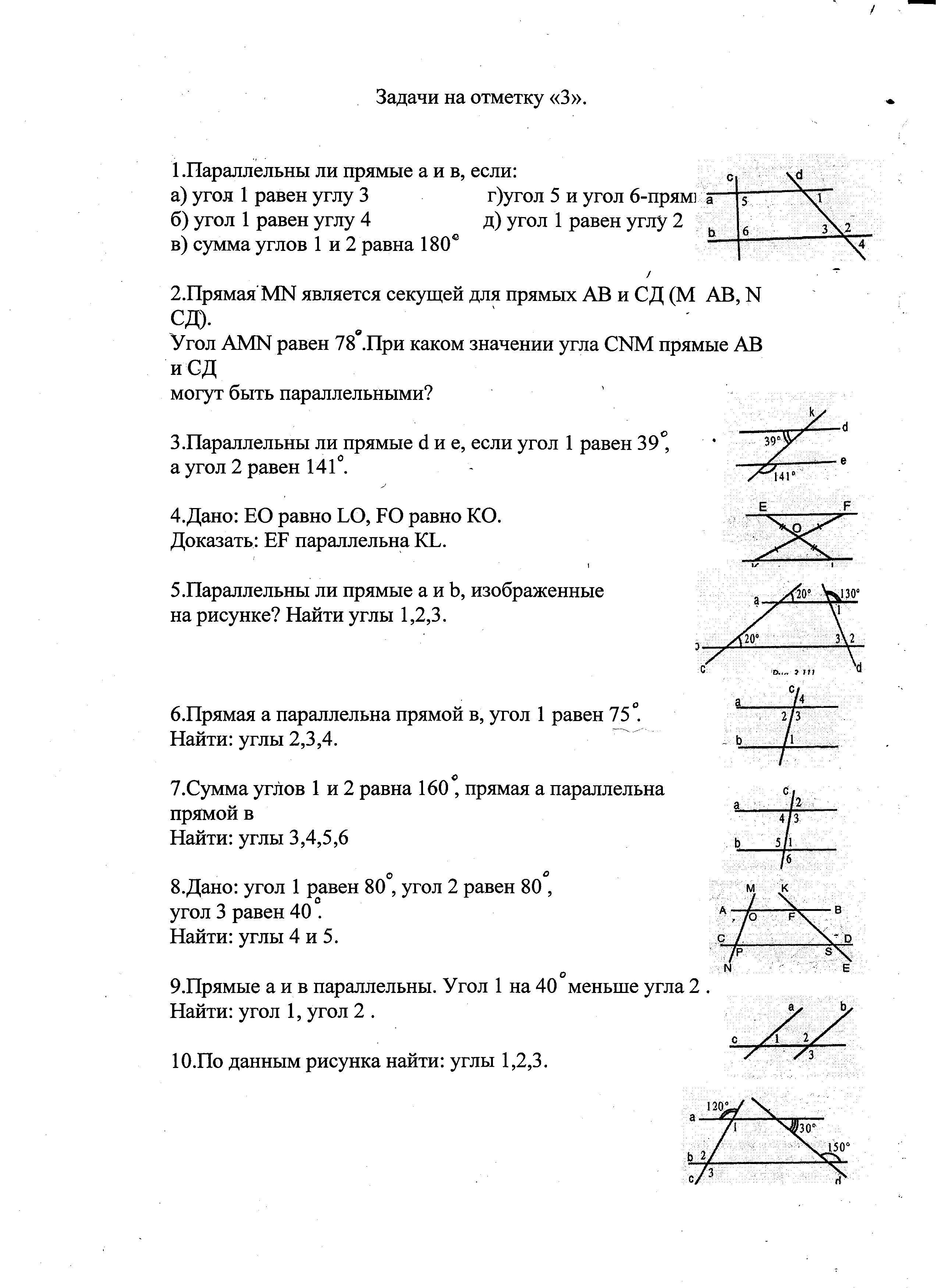
Задачи на отметку «3»

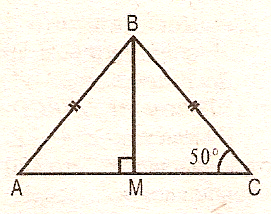1. Дан треугольник АВС. Сторона АВ равна стороне ВС,

Угол А равен 50°, ВМ- высота.

Найти: угол СВМ.

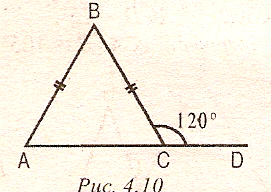2.Дан треугольник АВС, сторона АВ равна 5см. АВ

равна ВС.

Угол ВСД равен 120°.

Найти: АС.

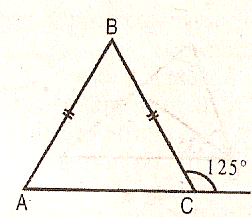3.Дан треугольник АВС. Сторона АВ равна стороне ВС.

Угол ВСД равен 125°.

Найти: угол А, угол В, угол С.

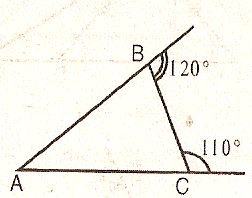4.Дан треугольник АВС. Внешние углы ДБС и ЕСВ

равны соответственно 120° и 110°.

Найти: угол А, угол В, уголС.

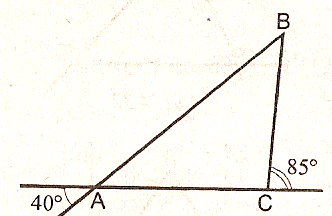5.Дан треугольник АВС. Угол 1 равен 40°,

угол 2 равен 85°.

Найти: угол А, угол В, угол С.

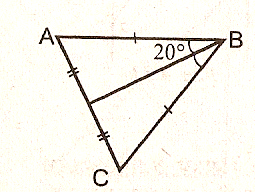6.Треугольник АВС- равнобедренный. ВД- биссектриса

угла АВС. Угол АВД равен 20°.

Найти: угол А, угол В, угол С.

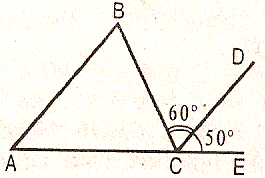7. Дан треугольник АВС. Сторона АВ параллельна

стороне СД. Угол ВСД равен 60°, угол ДСЕ равен 50°.

Найти: углы треугольника АВС.

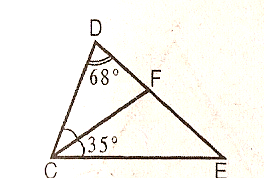8. В треугольнике СДЕ: СF- биссектриса, угол Д равен 68°,

угол FСЕ равен 35°.

Найти: угол Е, угол СFЕ.

9. Внутренние углы треугольника АВС пропорциональны числам 2, 5, 8.

Найти: углы треугольника АВС, внешние углы треугольника АВС

10. В треугольнике АВС проведена биссектриса ВД. Угол А равен 50°,

угол В равен 60°. Найти: углы треугольника СВД.