Классическая теория, основанная на нормальном законе распределения, при малых выборках неприменима. В этом случае используются другие законы распределения, разработанные микростатистикой: распределения Стьюдента и Фишера.
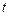 - распределение Стьюдента. Известно, что если из нормально распределенной совокупности значений случайной величины путем
- распределение Стьюдента. Известно, что если из нормально распределенной совокупности значений случайной величины путем 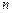 - кратного независимого выбора взять выборки объемом
- кратного независимого выбора взять выборки объемом 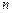 , то средние значения этих выборок будут тоже распределены нормально с тем же средним значением, но с меньшей дисперсией, т.е.
, то средние значения этих выборок будут тоже распределены нормально с тем же средним значением, но с меньшей дисперсией, т.е.
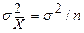 .
.
Отношение отклонения выборочного среднего значения 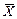 от его математического ожидания
от его математического ожидания 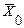 (среднее значение генеральной совокупности) к основной ошибке
(среднее значение генеральной совокупности) к основной ошибке 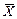 называется
называется 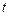 статистикой. Эта статистика имеет нормальное распределение с равным нулю средним значением и равной 1 дисперсией
статистикой. Эта статистика имеет нормальное распределение с равным нулю средним значением и равной 1 дисперсией
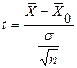 .
.
При научных исследованиях дисперсия генеральной совокупности 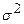 почти всегда неизвестна и поэтому нельзя выполнить нормирование. По выборке можно определить несмещенную оценку
почти всегда неизвестна и поэтому нельзя выполнить нормирование. По выборке можно определить несмещенную оценку 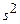 дисперсии
дисперсии 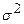
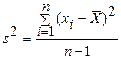 .
.
Отклонение выборочного среднего значения от среднего значения генеральной совокупности, нормированное при помощи этой оценки, называется 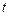 статистикой:
статистикой:
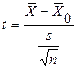 .
.
При 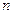 =30
=30 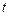 - распределение практически мало отличается от нормального распределения. При малых значениях
- распределение практически мало отличается от нормального распределения. При малых значениях 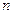
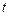 - распределение заметно отличается от нормального распределения. Оно более островершинное.
- распределение заметно отличается от нормального распределения. Оно более островершинное.
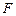 - распределение Фишера. Рассмотрим распределение статистики
- распределение Фишера. Рассмотрим распределение статистики 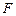 . Имеются две независимые выборки разных объемов, средние значения которых
. Имеются две независимые выборки разных объемов, средние значения которых 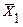 и
и 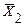 . По данным этих выборок получены оценки
. По данным этих выборок получены оценки 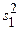 и
и 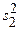 дисперсий генеральных совокупностей с числами свободы
дисперсий генеральных совокупностей с числами свободы 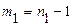 и
и 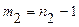 .
.
Требуется выяснить, являются ли эти оценки существенно различными, или данные выборки можно рассматривать как взятые наудачу из нормальных генеральных совокупностей, имеющих равные дисперсии 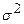 .
.
Для решения этой задачи применяется статистика 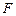 , называемая дисперсионным отношением. Статистика
, называемая дисперсионным отношением. Статистика 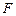 представляет отношение оценок
представляет отношение оценок 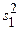 и
и 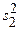 , полученных из независимых выборок, взятых наудачу из нормальных генеральных совокупностей с одинаковой дисперсией
, полученных из независимых выборок, взятых наудачу из нормальных генеральных совокупностей с одинаковой дисперсией 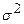 :
:
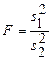 при
при 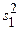 >
> 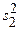 .
.
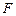 - распределение Фишера выражает вероятность того, что некоторое значение
- распределение Фишера выражает вероятность того, что некоторое значение 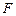 будет больше или равно
будет больше или равно 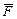 :
:
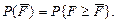
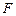 - распределение не зависит от дисперсии генеральной совокупности, а зависит от чисел степеней свободы. График плотности распределения приведен на рис. 1.8.
- распределение не зависит от дисперсии генеральной совокупности, а зависит от чисел степеней свободы. График плотности распределения приведен на рис. 1.8.
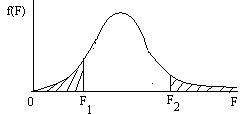
Рис. 1.8. 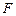 - распределение Фишера
- распределение Фишера
Статистика 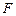 чаще всего применяется при дисперсионном анализе, в котором требуется только односторонний критерий значимости. Нулевая гипотеза, которая проверяется при помощи статистики
чаще всего применяется при дисперсионном анализе, в котором требуется только односторонний критерий значимости. Нулевая гипотеза, которая проверяется при помощи статистики 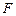 , состоит в том, что выборки взяты из одной нормальной генеральной совокупности или из разных нормальных генеральных совокупностей, имеющих равные дисперсии.
, состоит в том, что выборки взяты из одной нормальной генеральной совокупности или из разных нормальных генеральных совокупностей, имеющих равные дисперсии.
Распределения Фишера и Стьюдента используются при формировании выборки из выборок малого объема и установлении статистической значимости случайных величин, параметров и уравнений.
Малая выборка содержит мало информации об интересующем свойстве. Для получения более надежных выводов требуется объединить малые выборки в одну, но при этом необходимо установить их однородность. Совокупности однородны, если их математические ожидания равны.
Критериями для сравнения выборок служат: равенство двух выборочных дисперсий, равенство двух выборочных средних и однородность ряда выборочных дисперсий.
Критерий однородности ряда дисперсий. Однородность дисперсий ошибок измерений случайной величины в случае равного объема выборок оценивают по критерию Кохрена, расчетное значение которого определяют по формуле
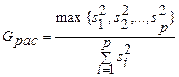 ,
,
где 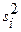 - дисперсия ошибок измерения СВ
- дисперсия ошибок измерения СВ 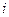 - й выборки;
- й выборки; 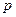 - число выборок.
- число выборок.
Критическое значение критерия определяют по таблице (приложение 1) при заданных значениях уровня значимости 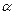 и степенях свободы:
и степенях свободы: 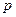 ;
; 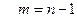 , где
, где 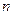 - число измерений (объем выборки).
- число измерений (объем выборки).
Пример 1.3. При определении предела прочности получены следующие значения дисперсий ошибок измерений пяти партий бетона: 2,5; 2,8; 3,2; 2,4; 2,7. Ошибки во всех случаях подсчитывались по 17 – ти измерениям.
Оценить однородность дисперсий ошибок измерений прочности, т.е. возможность проведения дисперсионного анализа.
Определяем расчетное значение критерия
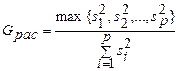 =
= 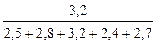 =0,235.
=0,235.
Критическое значение критерия при 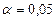 и
и 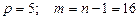 равно 0,3645. Таким образом,
равно 0,3645. Таким образом, 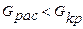 , гипотеза об однородности дисперсий ошибок измерений подтверждается с вероятностью 95 % и можно проводить дисперсионный анализ. Результаты расчета в среде ЭТ приведены в таблице 1.5.
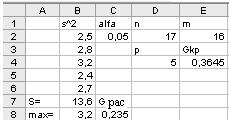
, гипотеза об однородности дисперсий ошибок измерений подтверждается с вероятностью 95 % и можно проводить дисперсионный анализ. Результаты расчета в среде ЭТ приведены в таблице 1.5.
Т а б л и ц а 1.5
Расчет в среде ЭТ
Критерий равенства двух дисперсий. Для сравнения дисперсий двух выборок используют 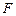 - критерий Фишера. Определяют расчетное значение
- критерий Фишера. Определяют расчетное значение 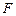 - критерия в виде отношения большей дисперсии к меньшей
- критерия в виде отношения большей дисперсии к меньшей
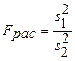 .
.
Так как проверяется гипотеза о равенстве генеральных дисперсий, то желательно, чтобы это отношение было как можно ближе к единице. Критическое значение 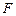 - критерия вычисляем с помощью статистической функции
- критерия вычисляем с помощью статистической функции 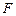 РАСПОБР. Число степеней свободы принимают соответственно
РАСПОБР. Число степеней свободы принимают соответственно 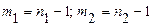 , где
, где 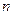 - объем выборки. Гипотеза о равенстве дисперсий подтверждается, если
- объем выборки. Гипотеза о равенстве дисперсий подтверждается, если 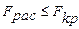 .
.
Критерий равенства двух средних. Для сравнения двух выборочных средних используют 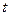 - статистику. После проверки гипотезы о равенстве двух выборочных дисперсий, вычисляют общую дисперсию двух выборок и расчетное значение
- статистику. После проверки гипотезы о равенстве двух выборочных дисперсий, вычисляют общую дисперсию двух выборок и расчетное значение 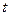 - статистики по формулам:
- статистики по формулам:
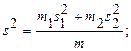
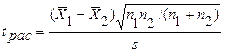 .
.
Критическое значение 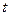 - статистики определяем с помощью статистической функции СТЬЮДРАСПОБР. Число степеней свободы
- статистики определяем с помощью статистической функции СТЬЮДРАСПОБР. Число степеней свободы 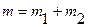 . Гипотеза о равенстве средних значений подтверждается, если
. Гипотеза о равенстве средних значений подтверждается, если 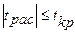 .
.
Пример 1.4. Сравним результаты испытаний двух выборок образцов бетона. В первой выборке объемом 29 образцов средний предел прочности 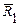 =40,1 МПа, дисперсия
=40,1 МПа, дисперсия 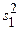 =8,2. Во второй выборке объемом 13 образцов средний предел прочности
=8,2. Во второй выборке объемом 13 образцов средний предел прочности 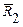 =40,9 МПа, дисперсия
=40,9 МПа, дисперсия 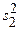 =7,1.
=7,1.
Расчетное значение 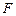 - критерия:
- критерия:
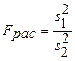 =8,2/7,1=1,155.
=8,2/7,1=1,155.
Диалоговое окно функции 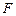 РАСПОБР представлено на рис. 1.9.
РАСПОБР представлено на рис. 1.9.
Степени свободы
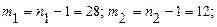
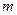 =28+12=40. Критические значения
=28+12=40. Критические значения 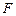 - критерия при различных значениях уровня значимости приведены в таблице 1.6.
- критерия при различных значениях уровня значимости приведены в таблице 1.6.
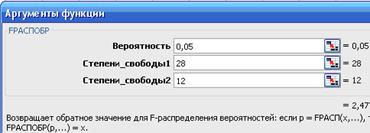
Рис. 1.9. Диалоговое окно функции FРАСПОБР
Т а б л и ц а 1.6
Результаты расчета в среде ЭТ
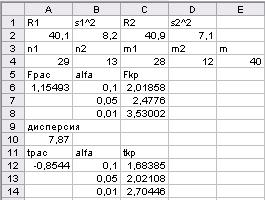
Так как расчетное значение 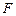 - критерия меньше критических значений при всех уровнях значимости, то гипотеза о равенстве дисперсий подтверждается.
- критерия меньше критических значений при всех уровнях значимости, то гипотеза о равенстве дисперсий подтверждается.
Определим общую дисперсию
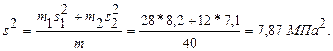
Вычислим расчетное значение 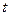 - статистики.
- статистики.
Критические значения 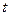 - статистики при различных значениях уровня значимости приведены в таблице 1.6.
- статистики при различных значениях уровня значимости приведены в таблице 1.6.
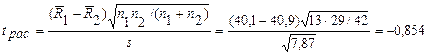 .
.
Расчетное значение 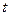 - статистики при всех уровнях значимости меньше критического значения. Следовательно, между средними значениями прочности бетона двух выборок нет существенного различия.
- статистики при всех уровнях значимости меньше критического значения. Следовательно, между средними значениями прочности бетона двух выборок нет существенного различия.
Для установления статистической значимости случайной величины определяют расчетное значение 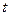 - статистики по формуле
- статистики по формуле
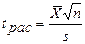
и сравнивают его с критическим значением 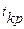 . Если
. Если 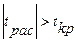 , то СВ статистически значима.
, то СВ статистически значима.
Пусть при испытании 5 – ти образцов оказалось, что среднее значение прочности на сжатие равно 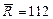 МПа, а стандартное отклонение
МПа, а стандартное отклонение 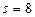 МПа.
МПа.
Расчетное значение
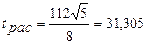 .
.
Критическое значение при 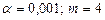 равно
равно 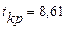 . Так как
. Так как 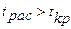 , то данное среднее значение прочности на сжатие статистически значимо.
, то данное среднее значение прочности на сжатие статистически значимо.
 2015-04-12
2015-04-12 1189
1189
