Теоретическая часть
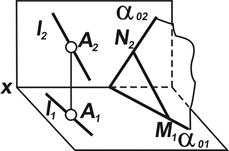 | · Прямая параллельна плоскости, если в плоскости возможно провести прямую, параллельную заданной (рис. 5.1). |
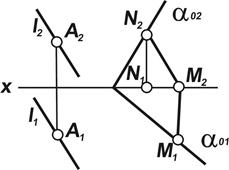 | · Прямая параллельна плоскости, если через нее возможно провести плоскость, параллельную заданной плоскости (рис. 5.1). |
| Рис. 5.1 | |
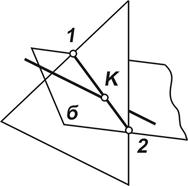 | 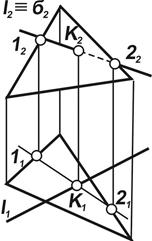 | · Если заданные прямая и плоскость имеют общее положение (рис. 5.2), то точку их пересечения находим в такой последовательности: Ø прямую заключаем в плоскость l 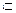 δ; δ δ; δ 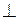 П2; Ø строим линию пересечения вспомогательной и заданной плоскости П2; Ø строим линию пересечения вспомогательной и заданной плоскости 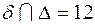 ; Ø находим точку встречи на пересечении полученной линии с заданной прямой К = ; Ø находим точку встречи на пересечении полученной линии с заданной прямой К = 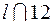 ; К = ; К = 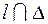 ; ; |
| Рис. 5.2 |
| Ø определяем видимость прямой методом конкурирующих точек. |
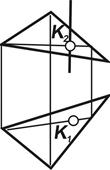 | 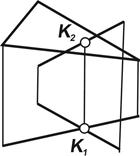 | · Если плоскость проецирующая, а прямая общего положения то точка пересечения находится на пересечении проекции прямой с проекцией плоскости занявшей проецирующее положение. · Если прямая занимает проецирующее положение, то точка пересечения определяется из условия принадлежности точки плоскости. |
| Рис. 5.3 |
| недостающие проекции определяются с помощью линий связи (рис. 5.3). |
ЗАДАЧИ
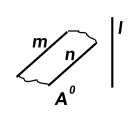
Задача 5.1. Через заданную точку провести произвольную прямую, параллельную данной плоскости (рис. 5.4…5.6).
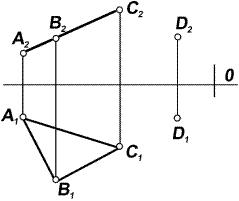 | 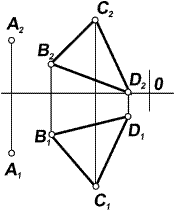 | 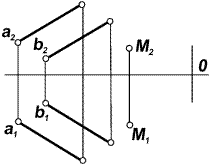 |
| Рис. 5.4 | Рис. 5.5 | Рис. 5.6 |
| | | | | |
Задача 5.2. Построить точку пересечения прямой с заданной плоскостью (рис 5.7; 5.8).
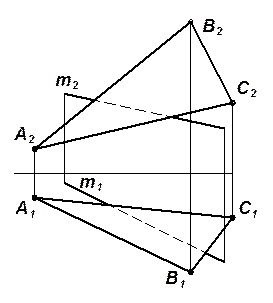 | 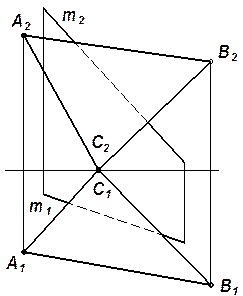 |
| Рис. 5.7 | Рис. 5.8 |
Задача 5.3. Через точку А провести прямую t, параллельную заданной плоскости 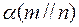 и пересекающую ℓ (рис. 5.9).
и пересекающую ℓ (рис. 5.9).
| Задача 5.4.Через точку А провести прямую, пересекающую обе заданные прямые m и n (рис. 5.10). | Задача 5.5. Провести прямую t, параллельную прямой ℓ и пересекающую прямые m и n (рис. 5.11). |
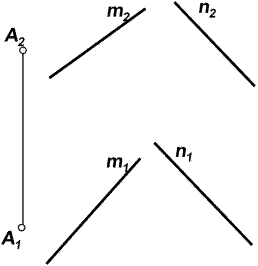 | 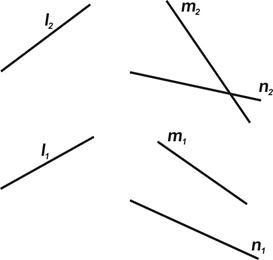 |
| Рис. 5.10 | Рис. 5.11 |
| |
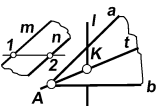
Указание. На рис. 5.12 представлены условия и решения
задач 5.4 и 5.5.
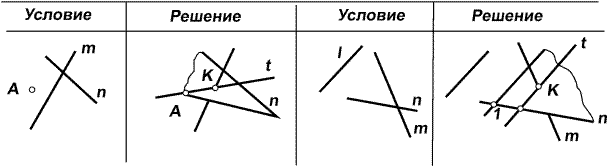 |
| Рис. 5.12 |




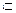 δ; δ
δ; δ 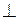 П2; Ø строим линию пересечения вспомогательной и заданной плоскости
П2; Ø строим линию пересечения вспомогательной и заданной плоскости 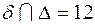 ; Ø находим точку встречи на пересечении полученной линии с заданной прямой К =
; Ø находим точку встречи на пересечении полученной линии с заданной прямой К = 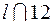 ; К =
; К =  ;
; 




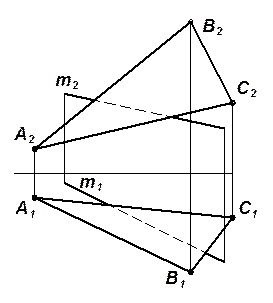
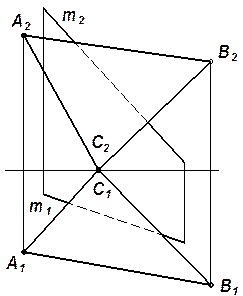
 и пересекающую ℓ (рис. 5.9).
и пересекающую ℓ (рис. 5.9).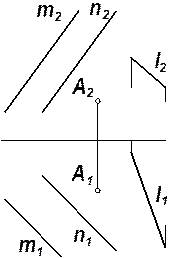



 2015-04-12
2015-04-12 721
721








