При разложении рациональной дроби на простейшие нужно найти неизвестные коэффициенты. Для этого простейшие дроби, стоящие в правой части равенств (1.4.5), (1.4.6), (1.4.7), (1.4.8), приводят к общему знаменателю. Тождественность этих равенств будет в том случае, если у них многочлены, стоящие в числителях слева и справа, будут равны. Поэтому у этих многочленов приравнивают числовые коэффициенты при одинаковых степенях х. Из полученной системы уравнений находят неизвестные коэффициенты.
Пример 7. Разложить на простейшие дроби:
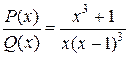
Знаменатель дроби имеет 4 корня: х 1 = 0, х 2,3,4 = 1, следовательно, данную дробь можно представить как сумму 4-х простейших дробей:
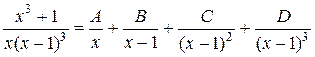 .
.
Приведем простейшие дроби в правой части равенства к общему знаменателю:
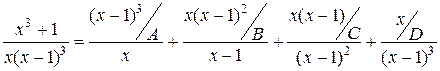
или
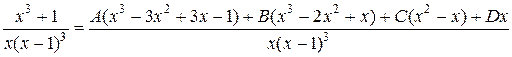 .
.
Приравниваем числовые коэффициенты при одинаковых степенях х и у многочленов, стоящих в числителе слева и сплава.
| х 3 | 1 = А + В |
| х 2 | 0 = –3 А – 2 В + С |
| х 1 | 0 = 3 А + В – С + D |
| х 0 | 1 = – А |
Из полученной системы уравнений находим неизвестные коэффициенты:
А = –1, В = 2, С = 1, D = 2.
Дробь разлагается на простейшие:
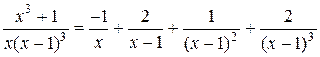 .
.
Пример 8. Разложить на простейшие дроби
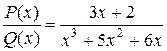
Найдем корни многочлена, стоящего в знаменателе:
x (х 2 + 5 x + 6) = 0; x 1 = 0; x 2 = –2; x 3 = –3.
Данная дробь равна сумме трех простейших дробей:
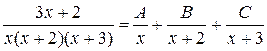 .
.
Приведем эти дроби к общему знаменателю
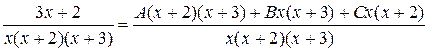 .
.
Освобождаясь от знаменателя, получим
3 х + 2 = А (х + 2)(х + 3) + Вх (х + 3) + Сх (х + 2).
В данном случае все три корня действительные и различные. Поэтому коэффициенты А, В, С можно найти другим способом. Подставим по очереди в последнее равенство значения всех трех корней:
| х = 0; | 2 = 6 А; | 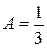 |
| х = –2; | –4 = –2 В; | В = 2 |
| х = –3; | –7 = 3 С; | 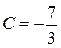 |
Дробь разлагается на простейшие:
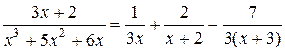 .
.
Задачи для самостоятельного решения. Разложить на простейшие дроби:
1. 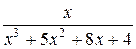 ;
;
2. 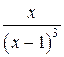 ;
;
3. 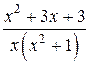 ;
;
4. 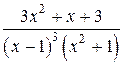 ;
;
5. 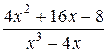 ;
;
6. 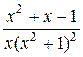 .
.
Практическое занятие 1.5. Интегрирование простейших дробей и рациональных функций
1.5.1. Интегрирование простейших дробей
Как уже отмечалось, рациональная функция – это отношение двух многочленов. Если она является неправильной дробью, то ее всегда можно представить в виде целой части (многочлена) плюс правильная рациональная дробь. В свою очередь правильную рациональную дробь, в зависимости от того, какие корни имеет многочлен знаменателя, разлагают на простейшие дроби 4-х видов:
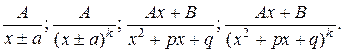
Интегралы от простейших дробей всех 4-х видов выражаются через элементарные функции:
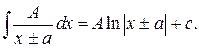
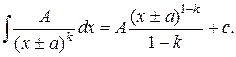
Интеграл вида 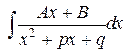 находят путем выделения полного квадрата в знаменателе, в результате он сводится к табличному.
находят путем выделения полного квадрата в знаменателе, в результате он сводится к табличному.
Пример 1. Найти интеграл 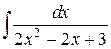 .
.
Решение. Вынесем в знаменателе 2 за скобку и выделим полный квадрат:
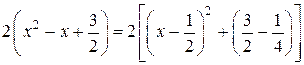 ;
;
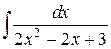 =
= 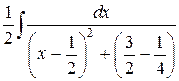 =
= 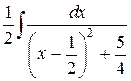 =
=
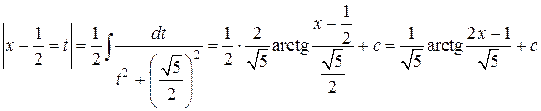 .
.
Пример 2. Найти интеграл 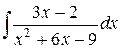
Решение. Выделяем в знаменателе полный квадрат:
x 2 + 6 x – 9 = 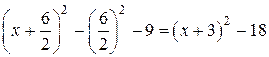 .
.
и вводим новую переменную t = x + 3.
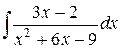 =
= 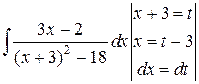 =
= 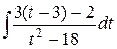 =
=
= 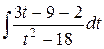 =
= 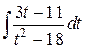 =
= 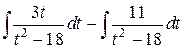 =
=
= 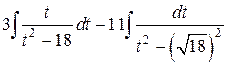 =
= 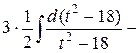
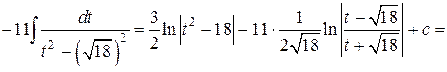
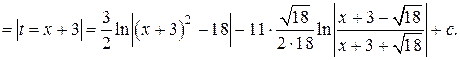
Метод нахождения интеграла 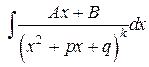 основан на приемах, ведущих к понижению степени квадратного трехчлена, стоящего в знаменателе. В общем случае вычисления очень громоздки, поэтому рассмотрим конкретный пример.
основан на приемах, ведущих к понижению степени квадратного трехчлена, стоящего в знаменателе. В общем случае вычисления очень громоздки, поэтому рассмотрим конкретный пример.
Пример 3. Вычислить интеграл:
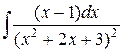
Выделим в числителе производную от знаменателя, тогда интеграл разобьется на два:
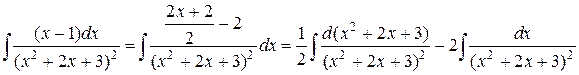 .
.
Первый 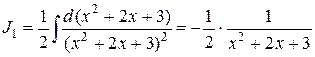 – является интегралом от степенной функции.
– является интегралом от степенной функции.
Второй 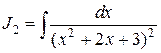 вычислим отдельно.
вычислим отдельно.
Понизим степень знаменателя у 2-го интеграла следующим образом:
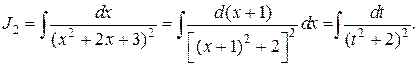
В числителе последнего интеграла прибавим и отнимем t2:
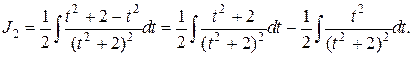
В результате интеграл J2 – снова разбился на два, один из которых является табличным, другой можно взять по частям:
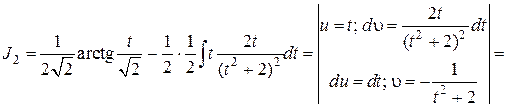
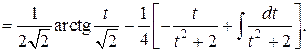
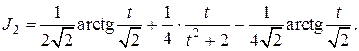
Итак: 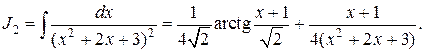
Подставим найденное значение J2 в исходное выражение, окончательно получим:
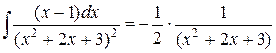
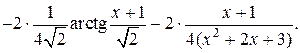
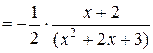
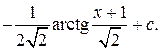
1.5.2. Интегрирование рациональных функций
Чтобы найти интеграл от рациональной дроби 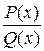 нужно:
нужно:
1. выделить целую часть, если рациональная функция является неправильной дробью;
2. у полученной правильной дроби найти корни многочлена, стоящего в знаменателе и по виду найденных корней записать правильную дробь в виде суммы простейших дробей с неизвестными коэффициентами;
3. найти неопределенные коэффициенты у простейших дробей;
4. проинтегрировать целую часть и простейшие дроби.
Пример 4. Вычислить интеграл
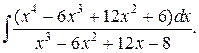
У рациональной функции, стоящей под знаком интеграла, степень многочлена числителя больше степени многочлена знаменателя.
Дробь неправильная, поэтому выделим целую часть:
| х 4 – 6 х 3 + 12 х 2 + 6 | х 3 – 6 х 2 + 12 х – 8 |
| х 4 – 6 х 3 + 12 х 2 – 8 х | х |
| +8 х + 6 |
Тогда исходный интеграл можно записать в виде:
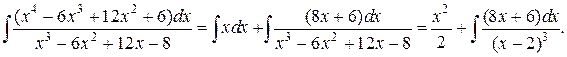
Знаменатель полученной правильной дроби, стоящий под знаком второго интеграла, имеет действительные кратные корни. Дробь разлагается на простейшие вида:
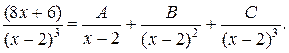
Чтобы найти коэффициенты А, В, С приведем простейшие дроби к общему знаменателю
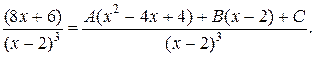
Приравняем коэффициенты при одинаковых степенях х у многочленов, стоящих в числителе слева и справа, получим:
| х 2 | 0 = А | А = 0 |
| х 1 | 8 = –4 А + В | В = 8 |
| х 0 | 6 = 4 А – 2 В + С | С = 22 |
проинтегрируем простейшие дроби.
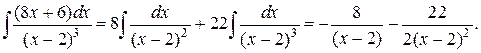
Подставляя в исходный интеграл, окончательно получим:
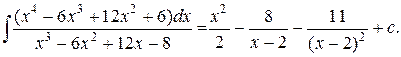
Пример 5. Найти 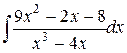 .
.
Решение. Дробь правильная, разложим знаменатель на множители так:
x 3 – 4 x = 0; x (x 2 – 4) = 0; x (x – 2)(x + 2) = 0;
x 3 – 4 x = x (x – 2)(x + 2).
Получили три множителя первой степени, соответствующие корням: 0, 2 и –2, каждый корень кратности 1.
Дробь разлагается на простейшие:
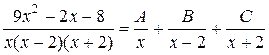
Умножим обе части разложения на общий знаменатель x (x – 2)(x + 2).

В результате получим
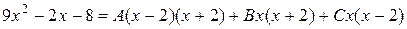 1.5.1.
1.5.1.
Общий знаменатель имеет три действительных корня. Подставляя каждый из них в левую и правую части равенства 1.5.1, найдем значения неизвестных коэффициентов А, В и С.
| x = 0, | 9×02 – 2×0 – 8 = A (0 – 2)(0 + 2) + B ×0×(0 + 2) + C×0×(0 – 2); –8 = –4 A Þ A = 2 |
| x = 2 | 9×22 – 2×2 – 8 = A ×(2 – 2)×(2 + 2) + B ×2×(2 + 2) + C ×2×(2 – 2), 9×4 – 4 – 8 = 0× A + 8× B + 0× C; 24 = 8 B Þ B = 3 |
| x = –2 | 9×(–2)2 – 2×(–2) – 8 = = A ×(–2 – 2)×(–2 + 2) + B ×(–2)×(–2 + 2) + C×(–2)×(–2 – 2); 9×4 + 4–8 = A ×0 + B ×0 + C×8; 32 = 8 C Þ C = 4 |
Итак: А = 2, В = 3, С = 4.
Эти же коэффициенты можно было получить другим способом.
Приравнивая коэффициенты при одинаковых степенях х слева и справа, в равенстве (1.5.1) получим систему уравнений:
| х 2 | 9 = А + В + С |
| х 1 | –2 = В .2 + С .(–2) |
| х 0 | –8 = А .(–4) |
Решая эту систему, находим те же значение коэффициентов
А = 2; В = 3; С = 4.
При решении обычно комбинируют оба метода.
Заменяя под знаком интеграла дробь ее разложением на простейшие дроби и находя интегралы, последовательно получаем
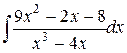 =
= 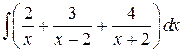 =
= 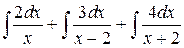 =
=
= 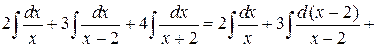
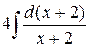 =
=
= 2×ln| x | + 3×ln| x – 2| + 4×ln| x + 2| + c.
Пример 6. Найти 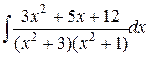 .
.
Решение. Знаменатель не имеет действительных корней, то есть разложен на множители второй степени.
Разложение подынтегральной дроби на простейшие имеет вид:
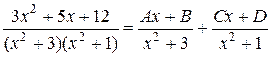 .
.
Умножив обе части полученного равенства на общий знаменатель 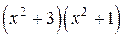 , получаем:
, получаем:
3 x 2 + 5 x + 12 = (Ax + B)(x 2 + 1) + (Cx + D)(x 2 + 3).
Приравнивая коэффициенты при одинаковых степенях x, будем иметь:
| х 3 | 0 = А + С |
| х 2 | 3 = В + D |
| х 1 | 5 = A + 3 C |
| х 0 | 12 = B + 3 D |
Решая систему, получаем: 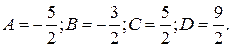
Интегрируя, находим:
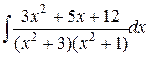 =
= 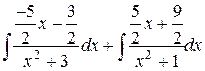 =
=
= 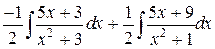 =
=
= 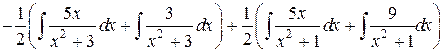 =
=
= 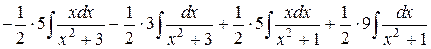 =
=
= 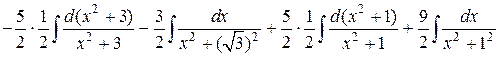 =
=
= 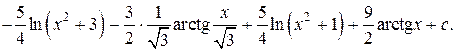
Пример 7. Найти 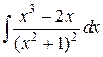 .
.
Решение. Так как 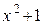 есть двукратный множитель, то
есть двукратный множитель, то
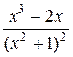 =
= 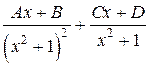 .
.
Освобождаясь от знаменателей, получим
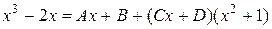 .
.
Приравниваем коэффициенты при одинаковых степенях х:
| х 3 | 1 = С |
| х 2 | 0 = D |
| х 1 | –2 = A + C |
| х 0 | 0 = B + D |
Решая систему получаем: A = –3, B = 0, C = 1, D = 0.
Следовательно,
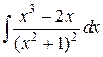 =
= 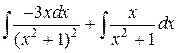 =
= 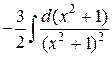 +
+
+ 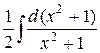 =
= 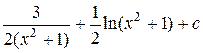 .
.
Заметим, что данный интеграл можно было найти проще с помощью подстановки 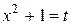 .
.
Пример 8. Найти интеграл 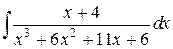 .
.
Решение. Так как подынтегральная функция является правильной дробью, то ее следует сразу представить в виде суммы простейших дробей. Легко видеть, что многочлен 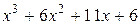 обращается в нуль при х =–1, поэтому он делится без остатка на х +1.
обращается в нуль при х =–1, поэтому он делится без остатка на х +1.
Выполним деление:
| x 3 + 6 x 2 + 11 x + 6 | x + 1 |
| x 3 + x 2 | x 2 + 5 x + 6 |
| 5 x2 + 11 x | |
| 5 x 2 + 5 x | |
| 6 x + 6 | |
| 6 x + 6 | |
Следовательно,
x 3 + 6 x 2 + 11 x + 6 = (x + 1)(x 2 + 5 x + 6) = (x + 1)(x + 2)(x + 3);
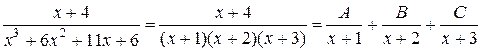 .
.
Освобождаясь от знаменателей, получим
x + 4 = A (x + 2)(x + 3) + B (x + 1)(x + 3) + C (x + 1)(x + 2).
Полагая х = –1, найдем 3 = 2 A, т.е. A = 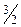 . Если х = –2, то получим
. Если х = –2, то получим
2= – B, т.е. B = –2. При х = –3 получим 1 = 2 С, т.е. С = 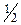 .
.
Итак,
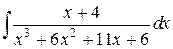 =
= 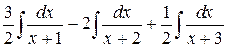 =
=
= 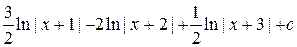 .
.
Пример 9. Найти интеграл 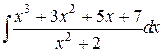 .
.
Решение. Выделим целую часть данной неправильной рациональной дроби:
| x 3 + 3 x 2 + 5 x + 7 | x 2 + 2 |
| x 3 + 2 x | x + 3 |
| 3 x 2 + 3 x + 7 | |
| 3 x 2 + 6 | |
| 3 x + 1 |
Итак,
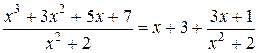 .
.
Отсюда находим
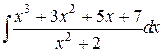 =
= 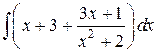 =
= 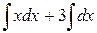 +
+
+ 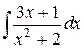 =
= 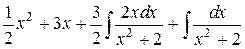 =
=
= 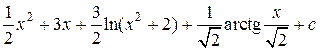 .
.
Пример 10. Найти интеграл 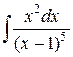 .
.
Решение. Подынтегральная функция является правильной рациональной дробью и можно было бы найти интеграл, представив эту дробь в виде суммы простейших дробей. Однако нахождение интеграла можно значительно упростить, если произвести замену переменной х – 1 = t; тогда x = t + 1 и dx = dt. В результате получаем
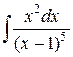 =
= 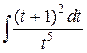 =
= 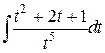 =
= 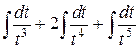 =
=
= 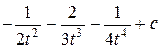 =
= 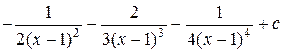 =
=
= 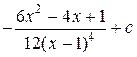 .
.
Иногда перед интегрированием рациональной дроби следует произвести замену переменной.
Задачи для самостоятельного решения. Найти интегралы:
134. 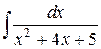 ; ; | 135. 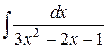 ; ; |
136. 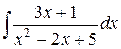 ; ; | 137. 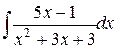 ; ; |
138. 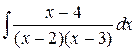 ; ; | 139. 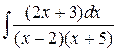 ; ; |
140. 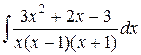 ; ; | 141. 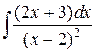 ; ; |
142. 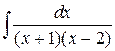 ; ; | 143. 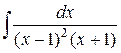 ; ; |
144. 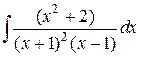 ; ; | 145. 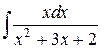 ; ; |
146. 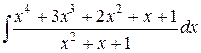 ; ; | 147. 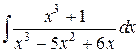 ; ; |
148. 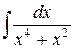 ; ; | 149. 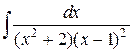 ; ; |
150. 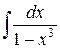 ; ; | 151. 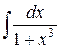 ; ; |
152. 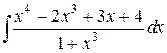 ; ; | 153. 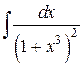 ; ; |
154. 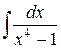 ; ; | 155. 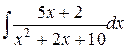 ; ; |
156. 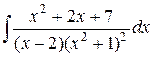 ; ; | 157. 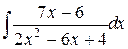 ; ; |
158. 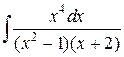 ; ; | 159. 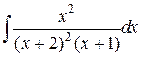 ; ; |
160. 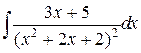 ; ; | 161. 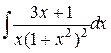 ; ; |
 2015-04-12
2015-04-12 2985
2985








