Два многочлена с действительными коэффициентами делят друг на друга по правилам, похожим на правила деления действительных чисел. Рассмотрим эту операцию на примере.
Пример 1. Разделим многочлен 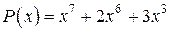 на многочлен
на многочлен 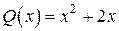
| x 7 + 2 х 6 + 3 х 3 | х 2 + 2 х | |
| x 7 + 2 х 6 | х 5 + 3 х – 6 | |
| 0 + 0 | ||
| 3 х 3 | ||
| 3 х 3 + 6 х 2 | ||
| 0 – 6 х 2 | ||
| – 6 х 2 – 12 х | ||
| 0 + 12 х | ||
Многочлен 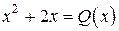 - называют делителем,
- называют делителем,
Многочлен 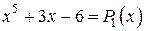 - частное,
- частное,
Многочлен 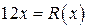 - остаток.
- остаток.
Задачи для самостоятельного решения. Разделить многочлен Р (х) на многочлен Q(x):
| 1. Р (х) = х 4 + 3 х 2 + 4; | Q (x) = x 2 – 3 x + 5 |
| 2. Р (х) = х 8 + х 7 – 3 х 4; | Q (x) = x 3 + 2 x 2 |
| 3. Р (х) = х 5 + х 4 – 8; | Q (x) = x 3 – 4 x |
1.4.1. Разложение многочлена на множители
Любой многочлен степени n имеет n -корней (действительных или комплексных) и его можно представить в виде произведения n -линейных сомножителей вида:
Рn (х) = bn (x – z 1) (x – z 2) (x – z 3)… (x – zn), (1.4.1)
где z 1, z 2, z 3 … zn – корни многочлена.
Если корни многочлена действительные и различные числа а 1, а 2, а 3 … аn, то он разлагается на линейные множители с действительными коэффициентами
Рn (х) = bn (x – а 1) (x – а 2) (x – а 3)… (x – аn). (1.4.2)
Когда в разложении (1.4.1) есть комплексный корень z = a + b i, то сопряженное ему комплексное число z = a – b i также будет корнем многочлена Р (х). Поэтому в разложении многочлена на линейные множители комплексные корни входят попарно сопряженными. Произведение таких двух сомножителей дает квадратный трехчлен с действительными коэффициентами:
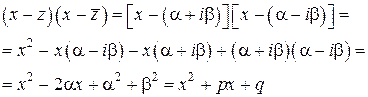
где р = –2a, q = a2 + b2.
В этом случае разложение многочлена Р (х) будет содержать линейные множители вида (х – а), соответствующие действительным корням, и квадратичные (х 2– рх+ q), соответствующие паре сопряженных комплексных корней:
Рn (х) = bn (x – а 1) … (x – аk) (x 2 + p 1 x + q 1)… (x 2 + pt x + qt). (1.4.3)
при этом k + 2 t = n.
Некоторые действительные корни могут быть равными. Если их k, то все такие сомножители можно объединить в одну скобку и записать как
(х – а) k.
Корень х = а называют корнем кратности k.
Среди квадратных множителей х 2 + рх + q тоже может встретиться t одинаковых, объединяя в одну скобку, их можно записать в виде (х 2 + рх + q) t – кратности t.
В результате разложение многочлена примет вид
Рn (х) = (x – а) k … (x 2 + px + q) t. (1.4.4)
Пример 2. Разложить на множители Р (х) = х 5 – 5 х 3 + 4 х.
Решение. Многочлен имеет пять корней. Найдем корни уравнения:
х (х 4 – 5 х 2 + 4) = 0.
Первый корень х 1 = 0. Чтобы найти остальные четыре корня, решим биквадратное уравнение:
х 4 – 5 х 2 + 4 = 0; x 2 = t; t 2 – 5 t + 4 = 0
D = 25 – 16 = 9; t 1 = 4; t 2 = 1.
Отсюда х 2 = 2, х 3 = –2, х 4 = 1, х 5 = –1.
Корни многочлена действительные и различные, следовательно
х 5 – 5 х 3 + 4 х = (х – 0) (х – 2) (х + 2) (х – 1) (х + 1).
Пример 3. Разложить на множители Р (х) = х 3 – 3 х 2 + 4.
Решение. Найдем корни уравнения х 3 – 3 х 2 + 4 = 0.
При решении подобных уравнений есть правило: если коэффициент при старшей степени равен единице, тогда целые корни такого многочлена, обязательно являются делителями свободного члена.
Число 4 делится на ± 1; ± 2; ± 4. Подставляем эти числа в уравнение: х 1 = –1; х 2 = 2 являются корнями. Для отыскания третьего корня используем правило кратности корня: если х = а является корнем кратности k многочлена Р (х), то Р (а) = Р' (а) = Р "(а) = … Р ( k – 1)(а) = 0; но Р ( k )(а) ≠ 0.
Производная (х 3 – 3 x 2 + 4)' = 3 х 2 – 6 х обращается в нуль при х = 2, т.е.
х = 2 двухкратный корень. Значит многочлен разлагается на множители
х 3 – 3 х 2 + 4 = (х + 1) (х – 2)2.
Пример 4. Разложить на множители Р (х) = х 4 – 16.
Решение. Многочлен имеет четыре корня. Запишем его в виде
Р (х) = (х 2 – 4) (х 2 + 4) = (х + 2) (х – 2) (х 2 + 4) первые два корня действительные х 1 = –2; х 2 = 2; третий и четвертый комплексные:
| х 2 + 4 = 0; | х 2 = –4; | 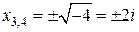 |
Отсюда разложение многочлена:
х 4 – 16 = (х + 2) (х – 2) (х 2 + 4).
Задачи для самостоятельного решения. Разложить на множители:
1. Р (х) = х 3 – х 2 + х – 1
2. Р (х) = х 4 – 6 х 2 + 8
3. Р (х) = х 3 – 6 х 2 + 12 х – 8.
1.4.2 Разложение рациональной функции на простейшие дроби
Определение. Отношение двух многочленов называют рациональной функцией или рациональной дробью:
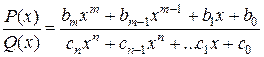 .
.
Если m ≥ n, то дробь неправильная.
Если m < n, то дробь правильная.
В случае неправильной дроби выделяют целую часть (многочлен Р (х) делят на многочлен Q (x)) в результате рациональная функция разбивается на две – целую часть (многочлен) и правильную рациональную дробь.
Правильную рациональную дробь 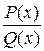 можно разложить на простейшие дроби 4-х видов в зависимости от того, какие корни имеет многочлен Q (x), стоящий в знаменателе.
можно разложить на простейшие дроби 4-х видов в зависимости от того, какие корни имеет многочлен Q (x), стоящий в знаменателе.
1. Если все корни многочлена Q (x) действительные и различные, то дробь 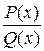 равна сумме простейших дробей такого вида:
равна сумме простейших дробей такого вида:
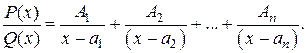 (1.4.5)
(1.4.5)
т.е. каждому действительному корню знаменателя соответствует одна простейшая дробь.
А 1, А 2, …, Аn – неизвестные коэффициенты, которые нужно найти.
Хотелось бы обратить особое внимание на форму записи простейших дробей: эти дроби должны быть правильными, т.е. степень многочлена числителя должна быть на единицу меньше степени многочлена знаменателя. Поскольку у простейших дробей знаменатели являются многочленами 1-й степени, то в числителе стоят числа А 1, А 2 … Аn (многочлены нулевой степени).
2. Если многочлен знаменателя Q (x) имеет кратные действительные корни, то рациональную дробь 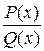 разлагают на простейшие дроби вида:
разлагают на простейшие дроби вида:
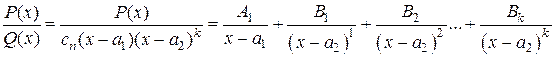 . (1.4.6)
. (1.4.6)
Во втором случае, как и в первом, число простейших дробей равно числу корней знаменателя, не смотря на то, что корень х = а 2 повторяется k -раз. В числителе всех простейших дробей также стоят многочлены 0-ой степени с неизвестными коэффициентами А 1, В 1, … Вk.
Пример 5. Представить в виде суммы простейших дробей рациональную дробь:
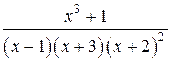 .
.
Знаменатель имеет 4 корня: из них корень х = –2 повторяется дважды. Поэтому дробь разлагается на четыре простейшие с неизвестными коэффициентами вида:
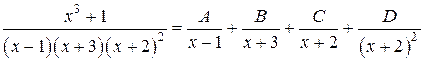 .
.
3. Если многочлен знаменателя Q (x) имеет комплексные корни, т.е. разлагается на квадратичные сомножители, то дробь 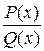 представляют сумной простейших дробей:
представляют сумной простейших дробей:
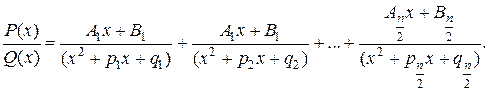 (1.4.7)
(1.4.7)
В третьем случае каждой паре сопряженных комплексных корней знаменателя соответствует одна простая дробь, поэтому число простейших дробей в два раза меньше, чем корней. Далее, у простейших дробей в знаменателе стоят многочлены 2-ой степени, следовательно, в числителе должны быть многочлены 1-ой степени с неизвестными коэффициентами А 1, А 2 … Аn /2; В 1, В 2 … Вn /2.
4. И наконец, если корни знаменателя комплексные и среди них есть кратные, то правильную рациональную дробь разлагают на простейшие вида:
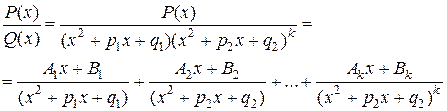 . (1.4.8)
. (1.4.8)
Пример 6. Представить в виде суммы простейших дробей:
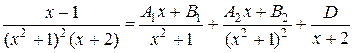 .
.
Задачи для самостоятельного решения. Представить в виде суммы простейших дробей:
1. 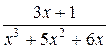 ;
;
2. 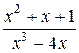 ;
;
3. 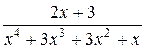 ;
;
4. 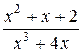 ;
;
5. 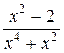 ;
;
6. 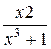 .
.
 2015-04-12
2015-04-12 4148
4148
