1.6.1. Интегралы вида 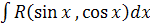 , где R – рациональная функция
, где R – рациональная функция
Интегралы указанного вида приводят к интегралам от рациональных функций с помощью так называемой универсальной тригонометрической подстановки 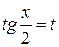 . В результате этой подстановки имеем:
. В результате этой подстановки имеем:
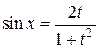 ;
; 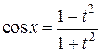 ; x = arctg t;
; x = arctg t; 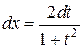 .
.
Пример 1. Найти 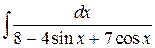 .
.
Решение. Воспользуемся универсальной тригонометрической подстановкой:
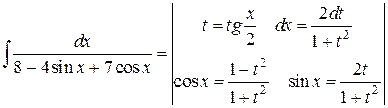 =
=
= 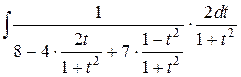 =
= 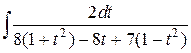 =
=
= 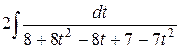 =
= 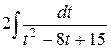 =
= 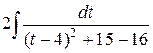 =
=
= 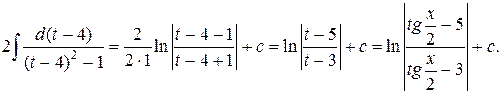
Пример 2. Найти 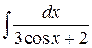 .
.
Решение. Воспользуемся универсальной тригонометрической подстановкой:
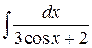 =
= 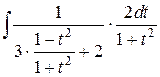 =
= 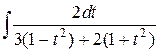 =
=
= 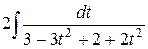 =
= 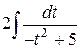 =
= 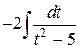 =
= 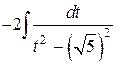 =
=
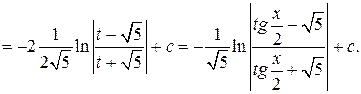
Универсальная подстановка 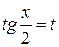 во многих случаях приводит к сложным вычислениям, т.к. при ее применении sin x и cos x выражаются через t в виде рациональных дробей, содержащих t 2.
во многих случаях приводит к сложным вычислениям, т.к. при ее применении sin x и cos x выражаются через t в виде рациональных дробей, содержащих t 2.
В некоторых частных случаях нахождение интегралов вида 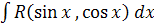 может быть упрощено.
может быть упрощено.
1. Если R (sin x, cos x) – нечетная функция относительно sin x, т.е.
R (–sin x, cos x) = – R (sin x, cos x),
то подынтегральная функция сводится к рациональной с помощью подстановки:
cos x = t, sin x = 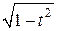 , x = arccost, dx =
, x = arccost, dx = 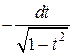 . (1.6.1)
. (1.6.1)
2. Если R (sin x, cos x) – нечетная функция относительно cos x, т.е.
R(sin x, –cos x) = –R(sin x, cos x),
то интеграл рационализируется подстановкой:
sin x = t, cos x = 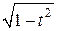 , x = arcsin t, dx =
, x = arcsin t, dx = 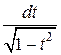 . (1.6.2)
. (1.6.2)
3. Если R (sin x, cos x) – четная функция относительно sin x и cos x, т.е.
R (–sin x, –cos x) = R (sin x, cos x),
то интеграл рационализируется подстановкой:
tg x = t, sin x = 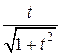 , cos x =
, cos x = 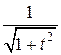 , x = arctg t, dx =
, x = arctg t, dx = 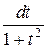 . (1.6.3)
. (1.6.3)
Пример 3. Найти 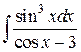 .
.
Решение. Заметим, что подынтегральная функция нечетная относительно sin x. Действительно 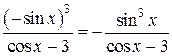 . Тогда удобнее воспользоваться подстановкой (1) cos x = t;
. Тогда удобнее воспользоваться подстановкой (1) cos x = t; 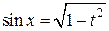 ;
; 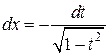
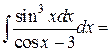
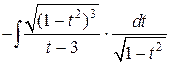 =
= 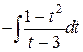 =
= 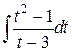
Под знаком интеграла неправельная дробь, выделим целую часть.
| t 2 – 1 | t – 3 |
| t 2 – 3 t | t + 3 |
| 3 t – 1 | |
| 3 t – 9 | |
Тогда 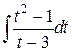 =
= 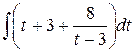 =
= 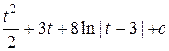 =
=
= 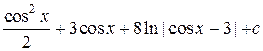 .
.
Пример 4. Найти 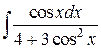 .
.
Решение. Заметим, что подынтегральная функция нечетная относительно cos x. Действительно 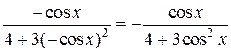 . Тогда удобнее воспользоваться подстановкой (2)
. Тогда удобнее воспользоваться подстановкой (2)
sin x = t, cos x = 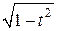 , x = arcsin t, dx =
, x = arcsin t, dx = 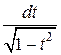 .
.
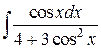 =
= 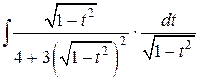 =
= 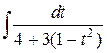 =
=
= 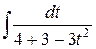 =
= 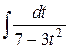 =
= 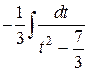 =
= 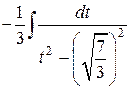 =
=
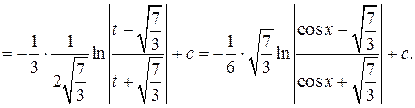
Пример 5. Найти 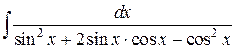 .
.
Решение. Подынтегральная функция четная относительно sin x и cos x. Действительно
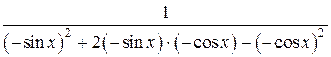 =
=
= 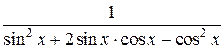 .
.
Тогда удобнее воспользоваться подстановкой (1.6.3)
tg x = t, sin x = 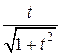 , cos x =
, cos x = 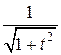 , x = arctg t, dx =
, x = arctg t, dx = 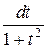 .
.
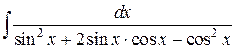 =
= 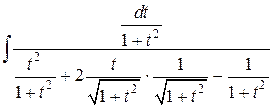 =
=
= 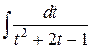 =
= 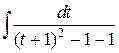 =
= 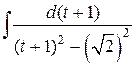 =
=
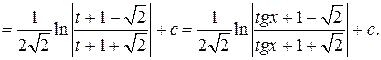
1.6.2. Интегралы вида 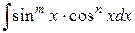 .
.
Выделим здесь два случая, имеющие особенно важное значение.
Случай 1. По крайней мере, один из показателей m или n – нечетное положительной число.
Если n – нечетное положительной число, то применяется подстановка sin x = t;
если m – нечетное положительное число, то применяется подстановка cos x = t.
Пример 6. Найти 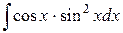 .
.
Решение. В нечетной степени cos x, значит используем подстановку
sin x = t.
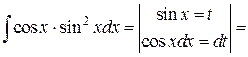
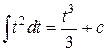 =
= 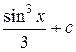 .
.
Пример 7. Найти 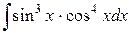 .
.
Решение. В нечетной степени sin x, следовательно используем подстановку cos x = t.
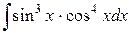 =
= 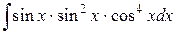 =
= 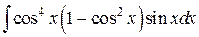 =
=
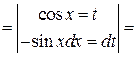
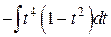 =
= 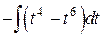 =
= 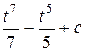 =
=
= 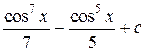 .
.
Случай 2. Оба показателя степени m и n – четные положительные числа. Здесь следует преобразовать подынтегральную функцию с помощью формул понижения степени:
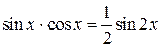 , (1.6.4)
, (1.6.4)
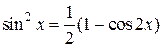 , (1.6.5)
, (1.6.5)
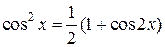 . (1.6.6)
. (1.6.6)
Пример 8. Найти 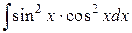 .
.
Решение. Из формулы (4) следует, что
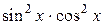 =
= 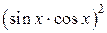 =
= 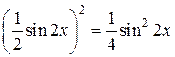 .
.
Применив теперь формулу (5), получаем:
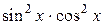 =
= 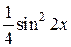 =
= 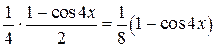 .
.
Итак,
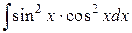 =
= 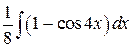 =
=
= 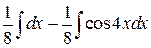 =
= 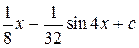 .
.
1.6.3. Интегралы вида 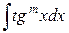 и
и 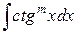 , где m – целое положительное число.
, где m – целое положительное число.
При нахождении таких интегралов применяются формулы
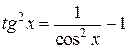 ,
, 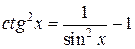 ,
,
с помощью которых последовательно понижается степень тангенса и котангенса.
Пример 9. Найти 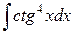 .
.
Решение.
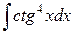 =
= 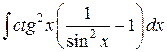 =
= 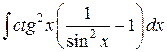 =
=
= 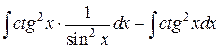 =
= 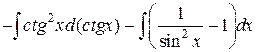 =
=
= 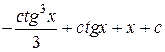 .
.
4. Интегралы вида 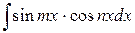 ,
, 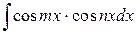 ,
,
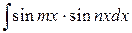 .
.
Тригонометрические формулы
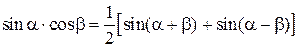 , (1.6.7)
, (1.6.7)
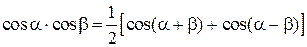 , (1.6.8)
, (1.6.8)
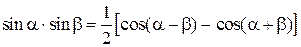 . (1.6.9)
. (1.6.9)
дают возможность произведение тригонометрических функций представить в виде суммы или разности.
Пример 10. Найти 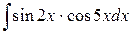 .
.
Решение. Используя формулу (1.6.7), получим
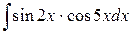 =
= 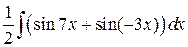 =
= 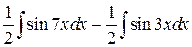 =
=
= 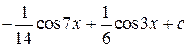 .
.
Пример 11. Найти 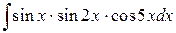 .
.
Решение. Применим к произведению sin x × sin 2x формулу (1.6.9)
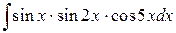 =
= 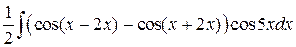 =
=
= 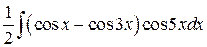 =
= 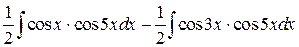 .
.
Применим формулу (1.6.8):
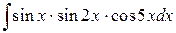 =
= 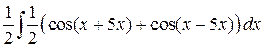 –
–
– 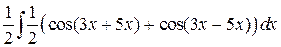 =
=
= 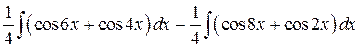 =
=
= 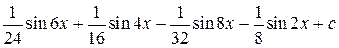 .
.
Задачи для самостоятельного решения. Найти интегралы.
194. 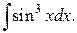 | 195. 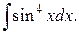 |
196. 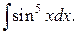 | 196. 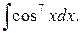 |
198. 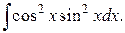 | 199. 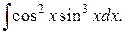 |
200. 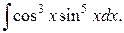 | 201. 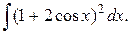 |
202. 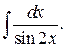 | 203. 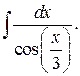 |
204.. 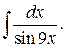 | 205. 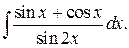 |
206. 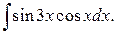 | 207. 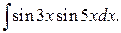 |
208. 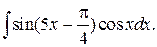 | 209. 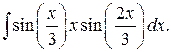 |
210.. 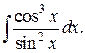 | 211. 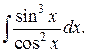 |
212. 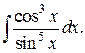 | 213. 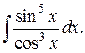 |
214. 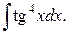 | 215. 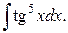 |
216. 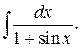 | 217. 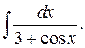 |
218. 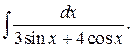 | 219. 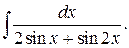 |
220. 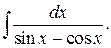 | 221. 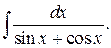 |
222. 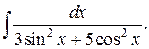 | 223. 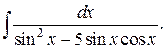 |
224. 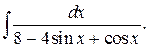 | 225. 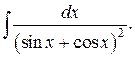  |
226. 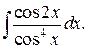 | 227. 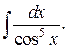 |
228. 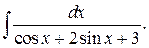 | 229. 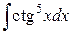 |
230. 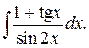 | 231. 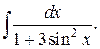 |
 2015-04-12
2015-04-12 3023
3023
