Практическое занятие 2.1. Линейный интеграл. Формула Ньютона-Лейбница. Замена переменной. Интегрирование по частям
2.1.1. Формула Ньютона-Лейбница
Существует несколько типов определенных интегралов в зависимости от вида области интегрирования (лекция 3.6).
Если интегрируемая функция задана на точках прямой, интеграл называют линейным. Он равен пределу интегральной суммы, т.е. числу, его записывают:
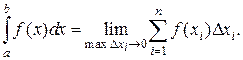
 (2.1.1)
(2.1.1)
Интервал от а до b называют интервалом интегрирования. При вычислении линейного интеграла пользуются формулой Ньютона-Лейбница, согласно которой линейный интеграл равен приращению любой из первообразных для функций f(x) на интервале интегрирования [ a; b ]:
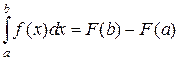 (2.1.2)
(2.1.2)
Разность значений функции F (x) часто записывают так:
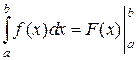 (2.1.3)
(2.1.3)
где знак 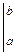 – означает, что в функцию F (x) надо подставить вместо аргумента сначала верхний предел, затем нижний и из первого результата вычесть второй.
– означает, что в функцию F (x) надо подставить вместо аргумента сначала верхний предел, затем нижний и из первого результата вычесть второй.
Найдем несколько простых интегралов с помощью полученной формулы.
Пример 1. 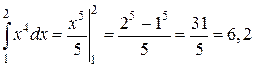
Пример 2. 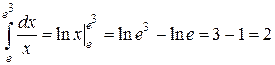
Пример 3. 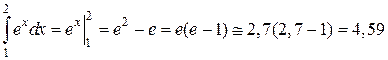
Пример 4. 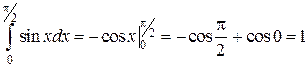
Пример 5. 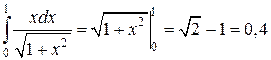
До сих пор считалось, что нижний предел в линейном интеграле 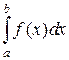 меньше верхнего (α < b).
меньше верхнего (α < b).
|
|
|
Для ряда случаев удобно распространить определение линейного интеграла, когда α > b. Если α > b, то будем считать, что
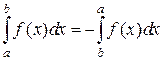 .
.
Далее следует отметить, что вычисление линейного интеграла с помощью неопределенного по формуле Ньютона-Лейбница на практике не всегда возможно. Во-первых, первообразная может не выражаться через известные элементарные функции, т.е. не берется соответствующий неопределенный интеграл, либо первообразная не выражается через известные неэлементарные (специальные) функции. Во-вторых, найденная первообразная может оказаться очень громоздкой. И, наконец, функция, которую надо проинтегрировать, может быть задана не формулой, а например, таблицей значений или графиком. Во всех этих случаях линейный интеграл вычисляют приближенно с помощью численного интегрирования.
Задачи для самостоятельного решения. Вычислить интегралы.
1. 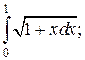
2. 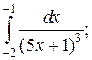
3. 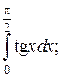
4. 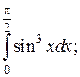
5. 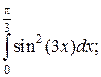
6. 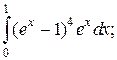
7. 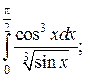
8. 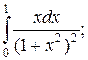
9. 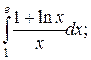
10. 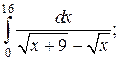
2.1.2. Замена переменной интегрирования в линейном интеграле
Переход к новой переменной интегрирования в определенном интеграле проводят по формуле:
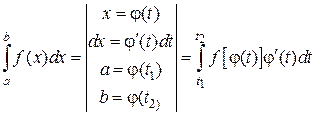 (2.1.4)
(2.1.4)
где функция х = φ(t) – должна быть дифференцируемой, а обратная t = ψ(х) – однозначной. Подынтегральное выражение в формуле (2.1.4) преобразуется так же, как в неопределенном интеграле. Однако очень важно подчеркнуть, что одновременно с преобразованием подынтегрального выражения, следует пересчитать пределы интегрирования, так как у новой переменной t будут другие границы изменения. Эти границы находят из уравнений:
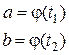
Уравнения получают путем подстановки х = α, х = b в функцию х = ψ(t). Возвращаться к старой переменной x, как это было в случае неопределенного интеграла, здесь не нужно.
|
|
|
Пример 6. Вычислить интеграл: 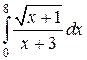 .
.
Чтобы избавиться от корня, возьмем его за новую переменную:
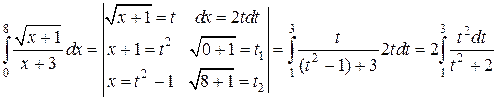
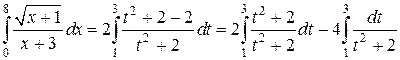
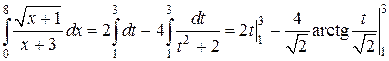
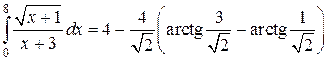
В приведенном примере новые пределы интегрирования 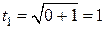 и
и 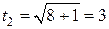 определяются однозначно, так как за новую переменную t взяты только положительные значения корня:
определяются однозначно, так как за новую переменную t взяты только положительные значения корня: 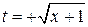 , т.е. функция
, т.е. функция
t = ψ(х) – однозначна.
Пример 7. Вычислить интеграл 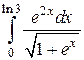
Как и в предыдущем примере за новую переменную возьмем квадратный корень.
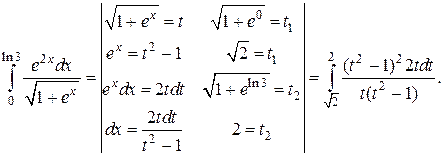
В результате интеграл сводится к двум табличным:
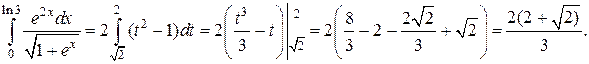
Задачи для самостоятельного решения. Вычислить интеграл.
1. 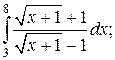
2. 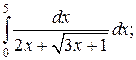
3. 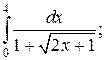
4. 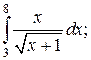
5. 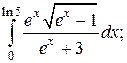
6. 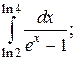
7. 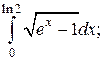
8. 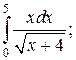
9. 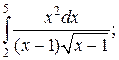
10. 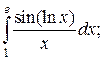
2.1.3. Интегрирование по частям в линейном интеграле
Нахождение первообразной методом интегрирования по частям в линейном интеграле проводят по той же формуле, что и в неопределенном интеграле:
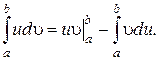
Разница заключается лишь в том, что для линейного интеграла находят не саму первообразную, а её приращение на интервале интегрирования [ α, b ].
Пример 8. Вычислить интеграл 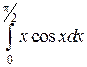 .
.
Решение. Разобьем на части подынтегральное выражение
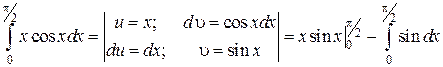
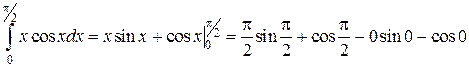
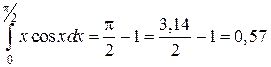
В данном случае соответствующий неопределенный интеграл берется. Значение линейного интеграла найдено по формуле Ньютона-Лейбница.
Задачи для самостоятельного решения. Вычислить интегралы.
1. 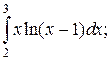
2. 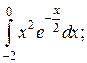
3. 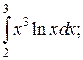
4. 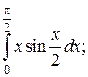
5. 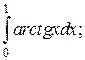
6. 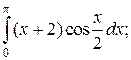
2.1.4. Приближенное вычисление линейного интеграла
Приближенное вычисление определенных интегралов по формулам прямоугольников, трапеций и Симпсона подробно рассмотрено в лекции 3.8. Вывод этих формул дан, исходя из геометрического смыла линейного интеграла, равного площади криволинейной трапеции.
В случае возрастающей функции на интервале [ a,b ], формула левых прямоугольников, дающая значение интеграла снедостатком, имеет вид:
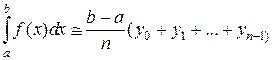 (2.1.4.1)
(2.1.4.1)
где у 0, у 1, …, уn -1 – значения подынтегральной функции в начале каждого частичного интервала.
Если значения функций берутся в конце частичных интервалов, то приближенное значение интеграла получают с избытком:
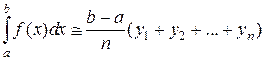 (2.1.4.2)
(2.1.4.2)
Формула правых прямоугольников. Обе формулы имеют сравнительно большую погрешность (первого порядка малости). Так для левых прямоугольников главный член погрешности на частичном интервале равен
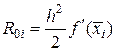 .
.
Суммирование по всему интервалу [ а, b ] дает общую ошибку
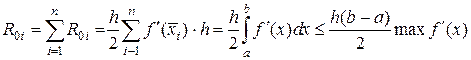 .
.
Если учесть, что 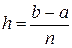 , то верхнюю границу абсолютной ошибки можно записать так
, то верхнюю границу абсолютной ошибки можно записать так
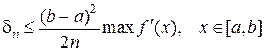 .
.
При уменьшении в два раза числа разбиений интервала [ а, b ] абсолютная ошибка возрастает также в два раза.
По сравнению с формулами (2.1.4.1) и (2.1.4.2) более точным является метод средних прямоугольников, т.е. когда значения функции f (х) вычисляют в срединах каждого частного интервала:
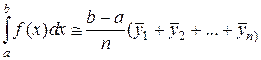 (2.1.4.3)
(2.1.4.3)
При этом верхняя граница абсолютной ошибки равна
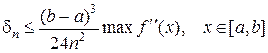 .
.
Если число точек (узлов) увеличить в два раза, точность формулы (2.1.4.3) улучшится в четыре раза. В самом деле
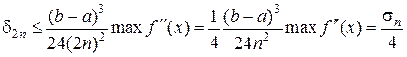 .
.
Однако, если подынтегральная функция f (х) определяется из эксперимента в дискретном наборе узлов, то метод средних прямоугольников применить нельзя из-за отсутствия значений f (х) в средних точках 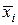 . В этом случае для интегрирования используют формулы трапеций и Симсона.
. В этом случае для интегрирования используют формулы трапеций и Симсона.
По формуле трапеций приближенное значение линейного интеграла равно
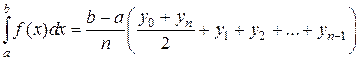 (2.1.4.4)
(2.1.4.4)
Абсолютная ошибка, которая получается при вычислении интеграла по этой формуле, не превосходит величины:
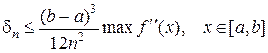 (2.1.4.5)
(2.1.4.5)
Однако, она в два раза больше по сравнению с методом средних прямоугольников. В обоих случаях, чем больше n – тем меньше ошибка.
На практике обычно трудно определить mах f" (х), поэтому для оценки верхней границы погрешности пользуются другим выражением:
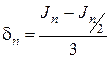 (2.1.4.6)
(2.1.4.6)
Формулу (2.1.4.6) получают следующим образом. Уменьшим число разбиений интервала [ а, b ] в два раза: n /2 и найдем, во сколько раз возрастет верхняя граница ошибки
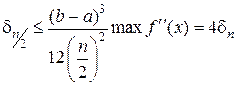
Точное значение линейного интеграла можно записать двумя способами
|
|
|
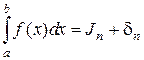 (2.1.4.7)
(2.1.4.7)
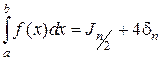 (2.1.4.8)
(2.1.4.8)
где Jn – приближенное значение интеграла, полученное при разбиении интервала [ а, b ] на n частей; Jn/ 2– приближенное значение интеграла при разбиении на 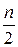 . Вычитая соответствующие части равенств (2.1.4.7) и (2.1.4.8), получим: 0 = Jn – Jn/ 2 – 3δ n.
. Вычитая соответствующие части равенств (2.1.4.7) и (2.1.4.8), получим: 0 = Jn – Jn/ 2 – 3δ n.
Откуда следует, что
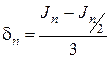 .
.
Формула парабол (формула Симпсона) имеет вид:
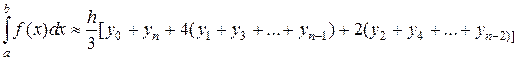 (2.1.4.9)
(2.1.4.9)
Формулу (2.1.4.9) называют формулой парабол или формулой Симпсона. Верхняя граница погрешности при вычислениях интеграла по этой формуле равна
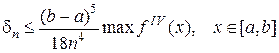 (2.1.4.10)
(2.1.4.10)
Погрешность имеет четвертый порядок малости. Формула Симпсона позволяет получить высокую точность, если четвертая производная подынтегральной функции не слишком велика. На практике в случае формулы Симпсона для δ n. Пользуется таким равенством:
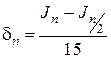 (2.1.4.11)
(2.1.4.11)
Его получают аналогично равенству (2.1.4.6). При уменьшении числа разбиений интервала [ а, b ] в два раза, верхняя граница ошибки возрастает в 16 раз:
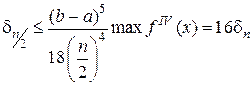 ,
,
поэтому 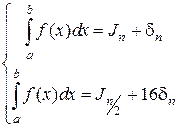 ; отсюда
; отсюда 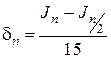 .
.
Пример. Вычислишь по формуле Ньютона-Лейбница и приближенно линейный интеграл:
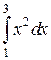
полученные результаты сравнить
1. Найдем точное значение данного интеграла по формуле Ньютона-Лейбница:
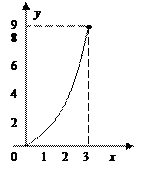 |
| Рис. 2.1.4.1 |
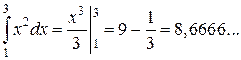
2. Построим график подынтегральной функции (рис. 2.1.4.1).
Разобьем интервал b – а = 3 – 1 = 2 на десять частей, т.е. n = 10
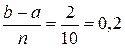
h = 0,2
Вычислим значения подынтегральной функции в точках: х 0 = 1; х 1= 1,2; х 2 = 1,4 и т.д., а также в срединах частичных интервалов. Результаты занесем в таблицу.
Таблица
| № | хi | у = х 2 | № | хi | у = х 2 | № | 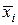 | 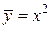 |
| х 0 | у 0 = 1 | х 0 | ||||||
| х 1 | 1,2 | у 1 = 1,44 | 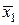 | 1,1 | 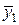 =1,21 =1,21 | |||
| х 2 | 1,4 | у 2 = 1,96 | х 1 | 1,4 | 1,96 | 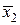 | 1,3 | 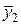 = 1,69 = 1,69 |
| х 3 | 1,6 | у 3 = 2,56 | 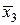 | 1,5 | 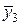 = 2,25 = 2,25 | |||
| х 4 | 1,8 | у 4 = 3,24 | х 2 | 1,8 | 3,24 | 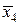 | 1,7 | 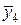 = 2,89 = 2,89 |
| х 5 | у 5 = 4 | 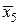 | 1,9 | 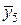 = 3,61 = 3,61 | ||||
| х 6 | 2,2 | у 6 = 4,84 | х 3 | 2,2 | 4,84 | 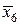 | 2,1 | 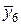 = 4,41 = 4,41 |
| х 7 | 2,4 | у 7 = 5,76 | 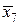 | 2,3 | 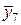 = 5,29 = 5,29 | |||
| х 8 | 2,6 | у 8 = 6,76 | х 4 | 2,6 | 6,76 | 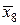 | 2,5 | 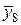 = 6,25 = 6,25 |
| х 9 | 2,8 | у 9 = 7,84 | 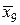 | 2,7 | 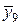 = 7,29 = 7,29 | |||
| х 10 | у 10 = 9 | х 5 | 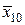 | 2,9 | 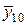 = 8,41 = 8,41 | |||
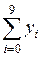 =39,4; =39,4; 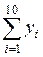 = 47,4 = 47,4 | 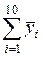 =43,3 =43,3 |
По формуле левых прямоугольников (с недостатком) находим
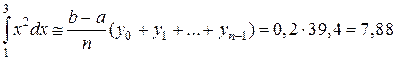
По формуле правых прямоугольников (с избытком) получим
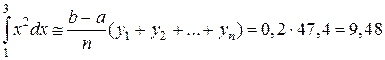 .
.
Результаты сильно отличаются от истинного значения, т.е. вычисления проведены с большой погрешностью. Найдем приближенное значение данного интеграла по формуле средних прямоугольников
|
|
|
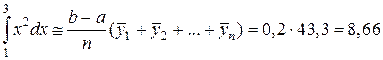 .
.
Результат весьма близкий к истинному.
Для сравнения вычислим приближенное значение данного интеграла по формулам трапеций и Симпсона.
По формуле трапеций для n = 10 с шагом h = 0,2 находим
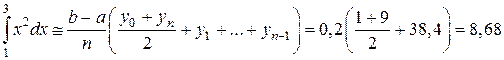
По формуле трапеций для 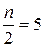 с шагом h = 0,4 получим
с шагом h = 0,4 получим
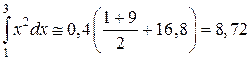 .
.
Верхняя граница абсолютной ошибки равна
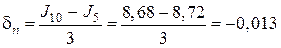
И, наконец, по формуле Симпсона для n = 10; h = 0,2
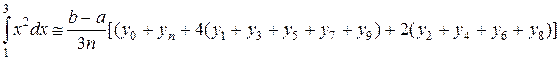
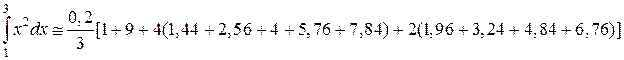
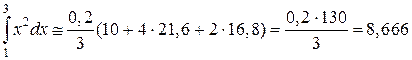 .
.
Как и следовало ожидать, самую высокую точность вычислений дает формула парабол (Симпсона), а затем формула средних прямоугольников.
Вычислить самостоятельно интеграл.
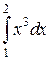
1) по формуле Ньютона-Лейбница;
2) по формуле левых и правых прямоугольников с шагом h = 0,1;
3) по формуле средних прямоугольников;
4) по формулам трапеций и Симпсона;
5) найти верхнюю границу погрешности для вычислений по формулам трапеций и Симпсона.
Практическое занятие 2.2. Несобственные интегралы I и II рода
Определенный линейный интеграл существует, если выполнены два условия, а именно:
1. интервал интегрирования конечен;
2. подынтегральная функция в интервале интегрирования нигде не обращается в бесконечность.
Такие определенные интегралы называют интегралами в собственном смысле этого слова, или собственными. Однако иногда приходится иметь дело с интегралами, у которых нарушено одно из этих условий. Они получили название несобственных.
2.2.1. Линейные интегралы с бесконечными пределами (I рода)
Дан определенный линейный интеграл:
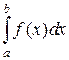
у которого f (x) – непрерывна на всей числовой оси 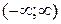 , и интервал интегрирования [ α,b ] – конечен. Пусть одна из границ интервала [ α,b ], или обе стремятся к бесконечности. Тогда пределы:
, и интервал интегрирования [ α,b ] – конечен. Пусть одна из границ интервала [ α,b ], или обе стремятся к бесконечности. Тогда пределы:
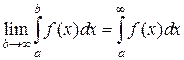
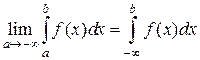
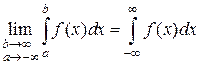
называют несобственными интегралами первого рода, или интегралами с бесконечными границами.
Если эти пределы равны конечному числу, то в таких случаях говорят, что несобственные интегралы первого рода сходятся.
Если пределы не существуют или равны бесконечности, то несобственные интегралы расходятся (не существуют).
Несобственные интегралы первого рода с одной бесконечной границей находят по формулам:
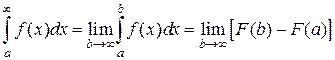
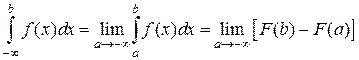
Поскольку под знаком пределов стоят определенные интегралы с конечными границами, их можно вычислять по формуле Ньютона-Лейбница (при условии, что соответствующий неопределенный интеграл берется), а затем найти предел полученного выражения.
Вычисление интеграла, у которого обе границы бесконечны, сводят к вычислению суммы двух несобственных интегралов с одной бесконечной границей:
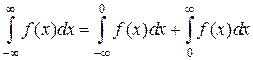
Вычислить несобственные интегралы:
Пример 1. 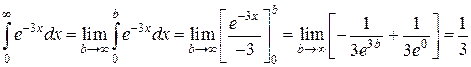
Интеграл сходится.
Пример 2. 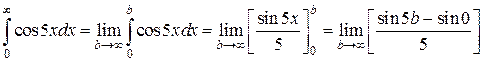
Функция sin5 b при 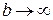 не имеет предела, интеграл расходится.
не имеет предела, интеграл расходится.
Пример 3. 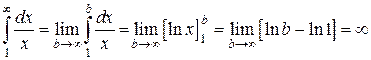
Интеграл расходится.
Пример 4. 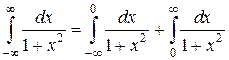
Вычислим каждый из двух интегралов с одной бесконечной границей:
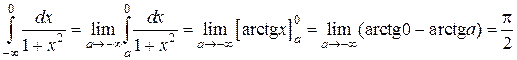
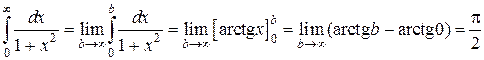 .
.
Складывая найденные значения двух несобственных интегралов, получим:
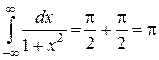 .
.
Данный интеграл сходится.
Пример 5. 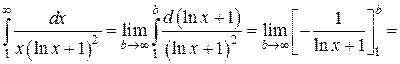
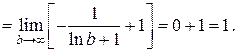
Интеграл сходится.
Пример 6. 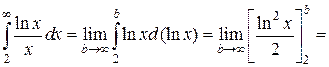
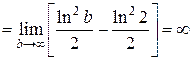
Интеграл расходится.
Пример 7. 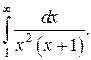
Разложим подынтегральную функцию на простейшие дроби.
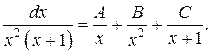
Приводя простейшие дроби к общему знаменателю и освобождаясь от него получим:
1 = А (х 2 + х) + В (х + 1) + Сх 2.
Приравняем числовые коэффициенты при одинаковых степенях х:
| х 2 | 0 = A + C; A = –C |
| х 1 | 0 = A + B; A = –B |
| х 0 | 1 = В |
Отсюда С = 1, А = –1, В = 1.
Заменим подынтегральную функцию суммой простейших дробей:
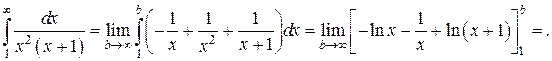
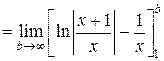
Применяя формулу Ньютона-Лейбница и вычисляя предел, окончательно получаем:
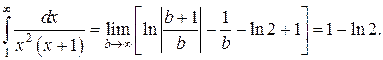
Интеграл сходится.
Пример 8. 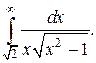
Сделаем замену переменной интегрирования:
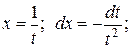 при
при 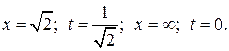
Тогда
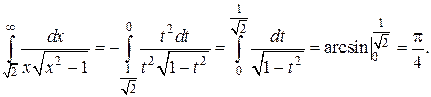
Интеграл сходится.
Задачи для самостоятельного решения. Вычислить интегралы.
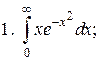
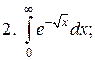
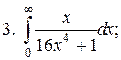
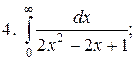
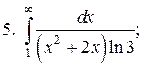
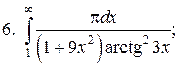
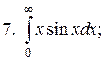
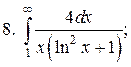
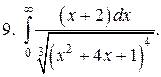
2.2.2. Линейные интегралы от разрывных функций, или несобственные интегралы второго рода
Рассмотрим интеграл 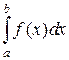 у которого интервал [ а,b ] конечен, а подынтегральная функция f (x) – терпит разрыв второго рода в одном из концов интервала (рис. 2.2.1).
у которого интервал [ а,b ] конечен, а подынтегральная функция f (x) – терпит разрыв второго рода в одном из концов интервала (рис. 2.2.1).
|
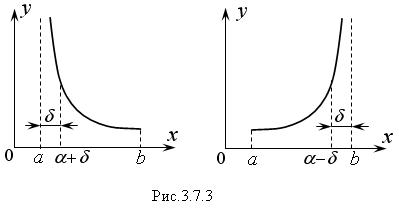
Изолируем точки бесконечного разрыва δ – окрестностью и рассмотрим такие пределы:
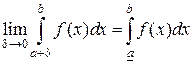
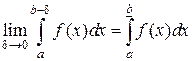
Эти пределы называют несобственными интегралами второго рода. Разрыв в одном из концов интервала обозначен символом «–».
В случае конечных пределов, говорят, что несобственные интегралы сходятся.
Если пределы не существуют или равны бесконечности, то несобственные интегралы расходятся.
Подынтегральная функция может иметь бесконечный разрыв в промежуточной точке х = с интервала [ α,b ]. Интеграл от такой функции разбивают на два несобственных интеграла второго рода:
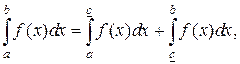
а < c < b,
Если оба интеграла в правой части равенства сходятся, то сходится и интеграл 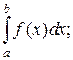 этот интеграл расходится, если расходятся хотя бы один из интегралов справа.
этот интеграл расходится, если расходятся хотя бы один из интегралов справа.
Интегралы от разрывных функций вычисляют по формулам, аналогичным для интегралов с бесконечными пределами:
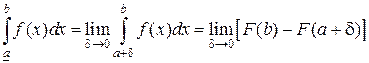
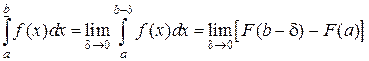
Пример 9. Вычислить несобственный интеграл 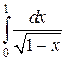 .
.
Решение. Подынтегральная функция обращается в бесконечность при
x = 1. Изолируем точку разрыва и найдем предел:

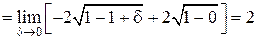
Интеграл сходится, т.е. существует.
Пример 10. Вычислить несобственный интеграл 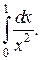
Решение. Функция 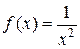 терпит разрыв второго рода в начале интервала [0,1]. Отступим от точки разрыва и найдем предел:
терпит разрыв второго рода в начале интервала [0,1]. Отступим от точки разрыва и найдем предел:
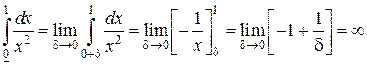
Данный интеграл расходится, или не существует.
Пример 11. Вычислить несобственный интеграл 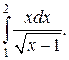
Решение. Подынтегральная функция терпит разрыв второго рода при
х = 1. Сделаем замену переменной интегрирования.
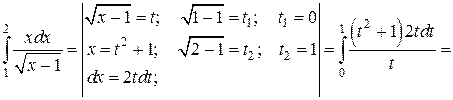
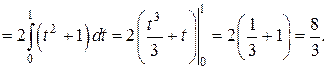
Интеграл сходится.
Пример 12. Вычислить интеграл 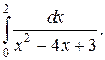
Решение. Квадратный трехчлен, стоящий в знаменателе, имеет два корня х = 1 и х = 3, и его можно записать в виде произведения двух литейных множителей (х – 1)(х – 3). Следовательно, подынтегральная функция терпит бесконечный разрыв внутри отрезка [0,2] при х = 1. Разобьем интеграл на два несобственных интеграла.
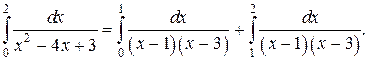
Разложим подынтегральную функцию на простейшие дроби:
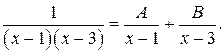
Освобождаясь от знаменателя получим:
1 = А (х – 3) + В (х – 1)
| при х = 1 | 1 = –2 А, | отсюда 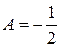 |
| при х = 3 | 1 = 2 В, | отсюда 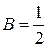 |
Найдем значение первого интеграла:
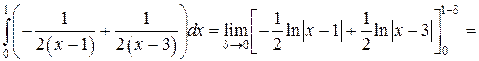
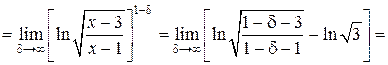
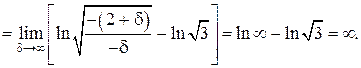
Интеграл расходится.
Задачи для самостоятельного решения. Вычислить интегралы.
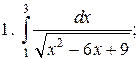
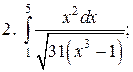
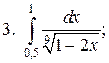
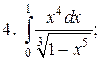
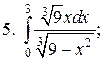
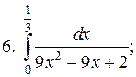
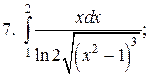
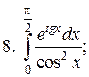
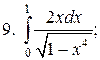
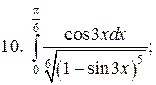
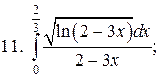
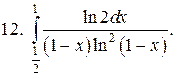
 2015-04-12
2015-04-12 5594
5594
