Свойство 1. Производная от неопределенного интеграла равна подынтегральной функции
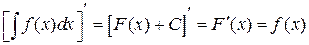 .
.
Свойство 2. Дифференциал от неопределенного интеграла равен подынтегральному выражению. В самом деле:
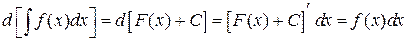 .
.
Свойство 3. Неопределенный интеграл от дифференциала функции равен самой функции плюс постоянная.
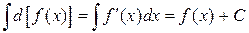 .
.
Из второго и третьего свойств следует, что символы дифференциала и неопределенного интеграла уничтожают друг друга, будучи примененными последовательно (если отвлечься от постоянного слагаемого в последней формуле).
Свойство 4. Интеграл от суммы конечного числа функций равен сумме интегралов от слагаемых функций:
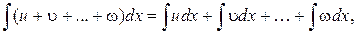
где u, υ,…, ω – функции независимой переменной х.
Свойство 5. Постоянный множитель подынтегральной функции можно вынести за знак интеграла, т.е.:
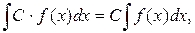
где С – константа.
Теорема. (Об инвариантности формул интегрирования). Всякая формула интегрирования сохраняет свой вид при подстановке вместо независимой переменной любой дифференцируемой функции от нее, т.е. если
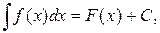 то и
то и 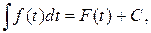
где t = φ (x) – любая дифференцируемая функция от х.
В силу этого правила таблица интегралов оказывается справедливой независимо от того, является ли переменная интегрирования независимой переменной или любой дифференцируемой функцией от нее.
1.2.2. Таблица интегралов
1. 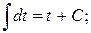
2. 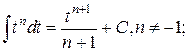
2а. 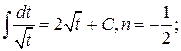
2б. 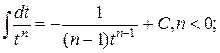
3. 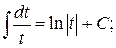
4. 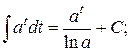
5. 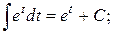
6. 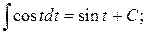
7. 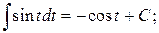
8. 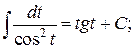
9. 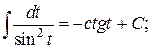
10. 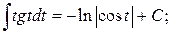
11. 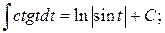
12. 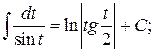
13. 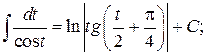
14. 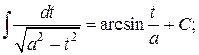
15. 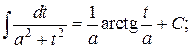
16. 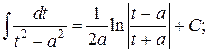 или
или 
17. 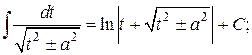
18. 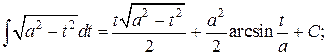
19. 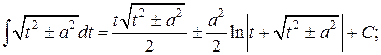
Таблица интегралов для элементарных функций выписана в предположении, что t может быть как независимой переменной, так и любой дифференцируемой функцией от х, т.е. t = φ(x).
Легко понять, что табличные интегралы можно было бы писать и в виде
3. 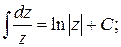 5.
5. 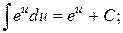 6.
6. 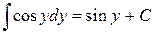 и т.п.
и т.п.
Сказанное делает понятным назначение множителя dx. Он указывает на переменную интегрирования: x, t, z, u, y.
Задача отыскания первообразной по заданной производной значительно труднее, чем нахождения производной от заданной функции. В основе всех приемов лежит одна цель - свести интеграл к табличному.
1.2.3. Непосредственное интегрирование
Суть непосредственного интегрирования состоит в том, что не определенный интеграл вычисляют с применением:
1) таблицы основных интегралов;
2) свойств интегралов;
3) тождественных элементарных преобразований подынтегрального выражения.
Пример 3. Найти интеграл 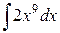
Решение. Воспользуемся свойством 5 неопределенного интеграла и формулой 2 таблицей основных интегралов:
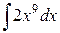 =
= 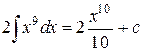 .
.
Пример 4. Найти интеграл 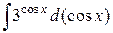
Решение. Используя формулу 4 таблицы основных интегралов и теорему об инвариантности формул интегрирования, находим
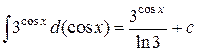
Пример 5. Найти интеграл 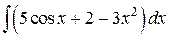 .
.
Решение. Применяя свойства 4 и 5, имеем
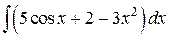 =
= 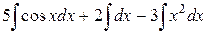 .
.
Используя, соответственно формулы 6,1,2 таблицы основных интегралов, находим
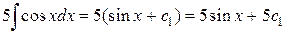 ;
;
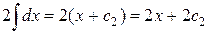 ;
;
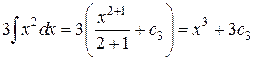 .
.
Таким образом,
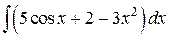 =
= 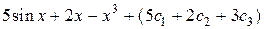 .
.
Обычно все произвольные постоянные суммируются, результат обозначают одной буквой: с =5 с 1+2 с 2+3 с 3, поэтому окончательно получаем
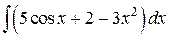 =
= 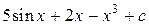 .
.
Пример 6. Найти интеграл 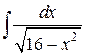 .
.
Решение. Интеграл табличный, поэтому можно переходить к не посредственному интегрированию по формуле 14, где а = 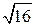 =4, получаем
=4, получаем
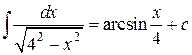 .
.
Пример 7. Найти интеграл 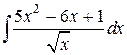 .
.
Решение. Интеграл не табличный, поэтому преобразуем его. Разделим числитель почленно на знаменатель и применим свойства 4 и 5.
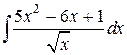 =
= 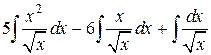 =
= 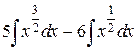 +
+
+ 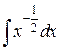 =
= 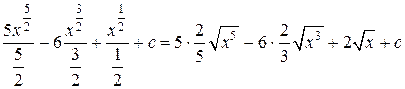 =
=
= 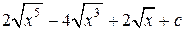 .
.
Использован табличный интеграл 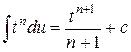 , n ¹–1.
, n ¹–1.
Пример 8. Найти интеграл 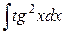 .
.
Решение. Интеграл не табличный. Воспользуемся тригонометрической формулой 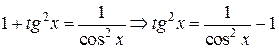 , а затем свойством 4
, а затем свойством 4
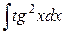 =
= 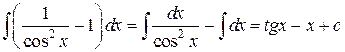 .
.
Применены табличные интегралы 8 и 1.
Задачи для самостоятельного решения. Найти интегралы:
1. 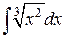 ; ; | 2. 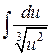 ; ; | |
3. 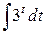 ; ; | 4. 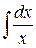 ; ; | |
5. 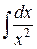 ; ; | 6. 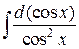 ; ; | |
7. 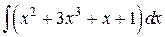 ; ; | 8. 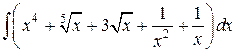 ; ; | |
9. 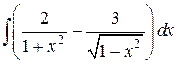 ; ; | 10. 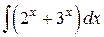 ; ; | |
11. 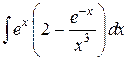 ; ; | 12. 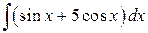 ; ; | |
13. 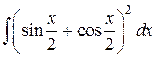 ; ; | 14. 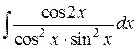 ; ; | |
15. 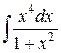 ; ; | 16. 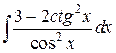 ; ; | |
17. 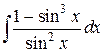 ; ; | 18. 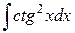 ; ; | |
19. 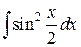 ; ; | 20. 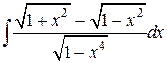 ; ; | |
21. 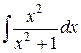 ; ; | 22. 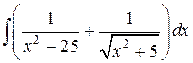 ; ; | |
23. 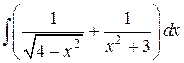 ; ; | 24. 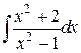 ; ; | |
25. 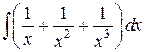 ; ; | 26. 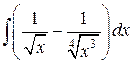 ; ; | |
27. 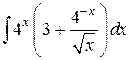 ; ; | 28. 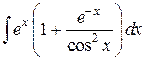 ; ; | |
29. 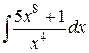 ; ; | 30. 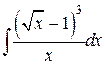 ; ; | |
31. 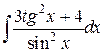 ; ; | 32. 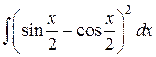 ; ; | |
33. 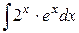 ; ; | 34. 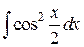 ; ; | |
35. 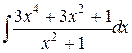 ; ; | 36. 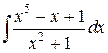 ; ; | |
37. 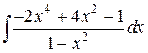 ; ; | 38. 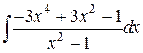 ; ; | |
39. 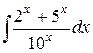 ; ; | 40. 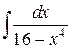 ; ; | |
41. 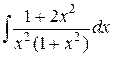 . . | ||
1.2.4. Интегрирование подведение под знак дифференциала
Применение теоремы об инвариантности формул интегрирования к нахождению первообразной называют методом подведения под знак дифференциала.
Этот метод применяют, когда под знаком интеграла стоит произведение двух функций, причем одна из них является производной от второй или её промежуточного аргумента. В этот случаи за переменную интегрирования можно взять функцию, производная от которой стоит под знаком интеграла, преобразовав соответственно дифференциал. Подведение производной под знак дифференциала и интегрирование по функции значительно расширяет основную таблицу интегралов.
Пример 1. Найти интеграл 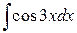 .
.
Решение. Интеграл не табличный. Заменим dx на 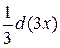 , т.е. внесем под знак дифференциала множитель 3 и разделим на него интеграл. В результате получаем
, т.е. внесем под знак дифференциала множитель 3 и разделим на него интеграл. В результате получаем
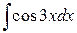 =
= 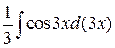 =
= 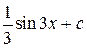 .
.
Пример 2. Найти интеграл 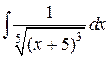 .
.
Решение. Интеграл не табличный.Преобразуем подынтегральную функцию
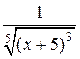 =
= 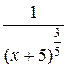 =
= 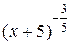 .
.
Так как dx=d (x +5) интеграл свелся к табличному от степенной функции
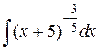 =
= 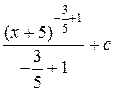 =
= 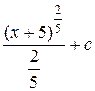 =
= 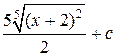 .
.
Пример 3. Найти интеграл 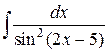 .
.
Решение. Интеграл не табличный. Заменим dx на 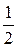 d (2 x –5). Получим
d (2 x –5). Получим
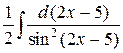 =
= 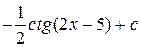 .
.
Использован табличный интеграл 9.
Пример 4. Найти интеграл 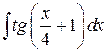
Решение. Заменим dx на 4 d (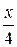 +1) u
+1) u
Воспользуемся табличным интегралом 10.
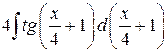 =
= 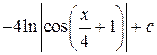 .
.
Пример 5. Найти интеграл 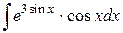 .
.
Решение. Заметим, что 3cos x – есть производная от 3sin x, т.е. 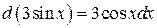 . Поэтому целесообразно ввести новую переменную 3sin x = u, тогда du =3cos xdx.
. Поэтому целесообразно ввести новую переменную 3sin x = u, тогда du =3cos xdx.
Итак, получим:
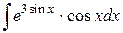 =
= 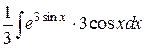 =
=
= 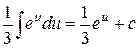 =
= 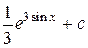 .
.
Использован табличный интеграл 5.
Пример 6. Найти интеграл 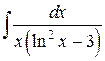 .
.
Решение. Заметим, что 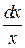 есть дифференциал от ln x, т.е. d(ln x) =
есть дифференциал от ln x, т.е. d(ln x) = 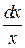 . Введем новую переменную u = ln x, тогда d u =
. Введем новую переменную u = ln x, тогда d u = 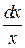 . Получим
. Получим
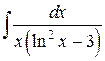 =
= 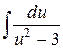 =
= 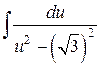 =
= 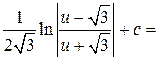 =
=
= 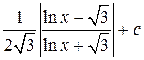 .
.
Использован табличный интеграл 16.
Пример 7. Найти интеграл 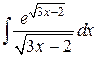 .
.
Решение. Заметим, что 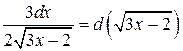 . Введем новую переменную u =
. Введем новую переменную u = 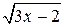 , тогда du =
, тогда du = 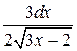 .
.
Получим
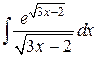 =
= 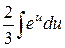 =
= 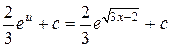 .
.
Использован табличный интеграл 5.
Пример 8. Найти интеграл 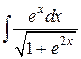 .
.
Решение. Заметим, что 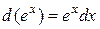 . Обозначим
. Обозначим 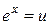 , du =
, du = 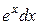 . Подставим эти выражения в интеграл и учтем, что
. Подставим эти выражения в интеграл и учтем, что 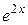 = (ex)2 = u 2.
= (ex)2 = u 2.
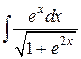 =
= 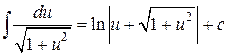 =
= 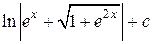 .
.
Использован табличный интеграл 17.
Пример 9. Найти интеграл 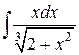 .
.
Решение.
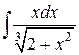 =
= 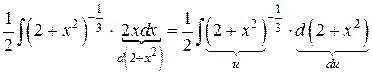 =
= 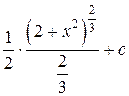 =
= 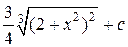 .
.
Пример 10. Вычислить 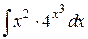 .
.
Решения.
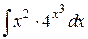 =
= 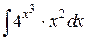 =
= 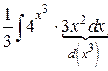 =
= 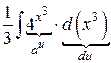 =
=
= 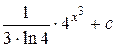 .
.
Использован табличный интеграл 4.
Пример 11. Вычислить 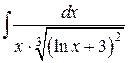 .
.
Решения.
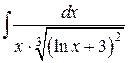 =
= 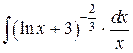 =
= 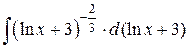 =
=
= 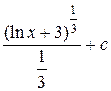 =
= 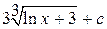 .
.
1.2.5. Замена переменной (метод подстановки)
Если подынтегральная функция такова, что трудно выделить производную от какого либо промежуточного аргумента или его просто нет, то в этом случае переменную интегрирования лучше заменить некоторой другой функцией, полагая х = y(t); dx = y'(t) dt, (предполагается, что y(t) и y'(t) непрерывны). Тогда
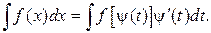
Если последний интеграл в результате такой замены свелся к табличному и равен F (t) + C, то исходный интеграл определяют путем возвращения к переменной х, т.е. из уравнения х = y(t) надо найти обратную функцию t = φ(х), и заменить t на φ(х).
С помощью подстановок такого рода удается избавится от корня, упростить подынтегральную функцию и свести интеграл к табличному. Однако, общего рецепта для выбора функции y(t) нет. В каждом конкретном случае её подбирают индивидуально по виду подынтегрального выражения. Все дальнейшее изложение темы «Неопределенный интеграл» будет состоять в основном из рассмотрения различных подстановок. Приведем несколько примеров.
Пример 1. Найти 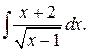 В данном интеграле нужно избавится от корня. Положим
В данном интеграле нужно избавится от корня. Положим 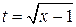 , тогда х = t 2+1; dx =2 tdt, интеграл примет вид
, тогда х = t 2+1; dx =2 tdt, интеграл примет вид
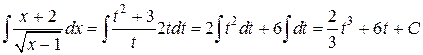 .
.
Заменяя t выражением 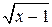 , окончательно получим
, окончательно получим
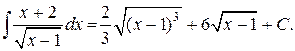
Пример 2. Найти 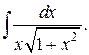 Положим
Положим 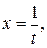
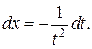
В результате такой замены интеграл сводится к табличному.
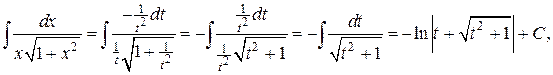
где 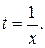 Заменяя t выражением
Заменяя t выражением 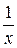 , окончательно получим
, окончательно получим
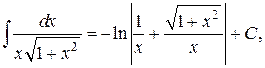
(можно было сделать подстановку х = tg t).
Пример 3. Вычислить 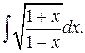 В данном интеграле также нужно избавиться от корня. Для этого оказывается удобной замена
В данном интеграле также нужно избавиться от корня. Для этого оказывается удобной замена 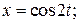
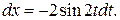
Выражение 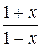 преобразуется так:
преобразуется так:
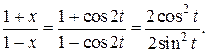
Интеграл примет вид:
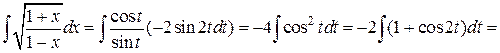
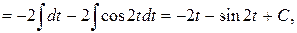
где 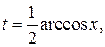 возвращаясь к переменной х, получим:
возвращаясь к переменной х, получим:
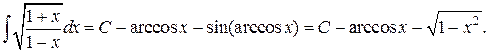
Задачи для самостоятельного решения. Вычислить
42. 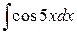 ; ; | 43. 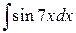 ; ; |
44. 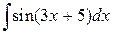 ; ; | 45. 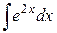 ; ; |
46. 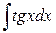 ; ; | 47. 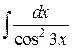 ; ; |
48. 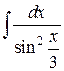 ; ; | 49. 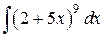 ; ; |
50. 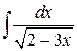 ; ; | 51. 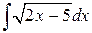 ; ; |
52. 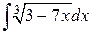 ; ; | 53. 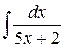 ; ; |
54. 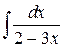 ; ; | 55. 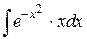 ; ; |
56. 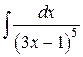 ; ; | 57. 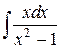 ; ; |
58. 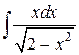 ; ; | 59. 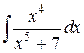 ; ; |
60. 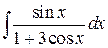 ; ; | 61. 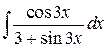 ; ; |
62. 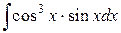 ; ; | 63. 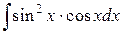 ; ; |
64. 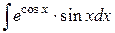 ; ; | 65. 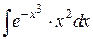 ; ; |
66. 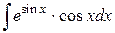 ; ; | 67. 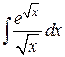 ; ; |
68. 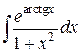 ; ; | 69. 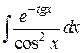 ; ; |
70. 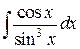 ; ; | 71. 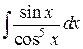 ; ; |
72. 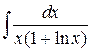 ; ; | 73. 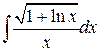 ; ; |
74. 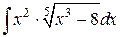 ; ; | 75. 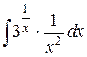 |
76. 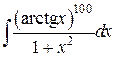 ; ; | 77. 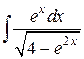 ; ; |
78. 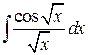 ; ; | 79. 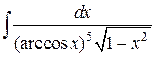 ; ; |
80. 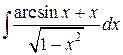 ; ; | 81. 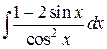 ; ; |
82. 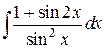 ; ; | 83. 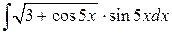 ; ; |
84. 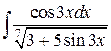 ; ; | 85. 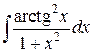 ; ; |
86. 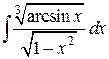 ; ; | 87. 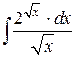 ; ; |
88. 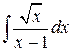 ; ; | 89. 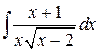 ; ; |
90. 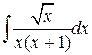 ; ; | 91. 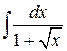 ; ; |
92 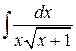 .; .; | 93. 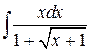 ; ; |
94. 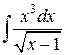 ; ; | 95. 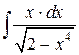 ; ; |
96. 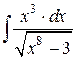 ; ; | 97. 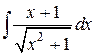 ; ; |
98. 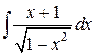 ; ; | 99. 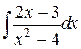 . . |
Практическое занятие 1.3. Метод интегрирования по частям
Метод интегрирования по частям следует из дифференцирования произведения двух функций. Известно, что
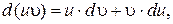 откуда
откуда
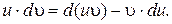
Интегрируя обе части последнего равенства, получим:
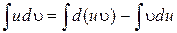 или
или
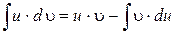 (1.3.1)
(1.3.1)
Выражение (1.3.1) является формулой интегрирования по частям.
Данный метод состоит в том, что подынтегральное выражение f (x)· dx представляется каким-либо образом в виде произведения двух множителей u и dυ. Множитель u, стоящий в левом интеграле, при переходе к правому интегралу заменяется на du, т.е. дифференцируется. Другой сомножитель dυ из левого интеграла заменяется на υ, т.е. интегрируется. Надо так подынтегральное выражение представить в виде произведения двух сомножителей, чтобы обе операции составили в совокупности задачу более простую, чем непосредственное вычисление интеграла 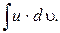 На практике чаще упрощение обусловлено дифференцированием множителя u.
На практике чаще упрощение обусловлено дифференцированием множителя u.
Если в составе подынтегрального выражения имеется множитель, упрощающийся от дифференцирования, то его следует взять за «u», а все остальное (включая dx!) за «dυ».
Пример 1. Вычислить 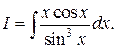 Ясно, что за «u» надо взять множитель х, так как при дифференцировании он «исчезает»
Ясно, что за «u» надо взять множитель х, так как при дифференцировании он «исчезает»
u = x, du = dx, 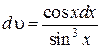 и
и 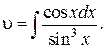
Чтобы найти 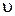 сделаем замену z = sin x; dz = cos xdx, тогда
сделаем замену z = sin x; dz = cos xdx, тогда
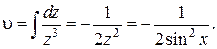
Когда применяют интегрирование по частям и по d υ находят υ, то произвольной постоянной не вводят, присоединяя ее к произвольной постоянной второго, незавершенного интегрирования в правой части равенства (1.3.1).
Применяя формулу (1.3.1), получим:
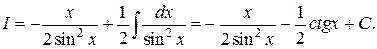
Пример 2. Вычислить 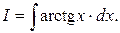 Здесь за «u» следует взять arctg x, тогда dυ = dx. Составим таблицу:
Здесь за «u» следует взять arctg x, тогда dυ = dx. Составим таблицу:
| u = arctg x | 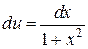 |
| dυ =dx | 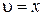 |
применяя формулу интегрирования по частям (1.3.1) получим:
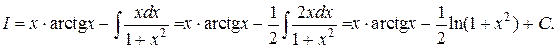
Пример 3. Вычислить интеграл 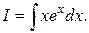 За «u» принимаем х, тогда
За «u» принимаем х, тогда
| u = х | du = dx |
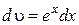 | 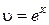 |
Применяя формулу (1.3.1) получим
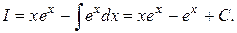
Иногда интегрирование по частям приходиться применять несколько раз.
Пример 4. Вычислить 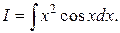
Разобьем подынтегральное выражение на части
| u = х 2 | du = 2 xdx |
| dυ = cos xdx | υ = sin x |
Тогда 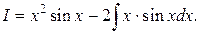
В последнем равенстве интеграл 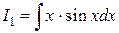 – проще исходного (то, что cos x заменился на sin x не изменяет сути решения, а вместо х 2 появился более простой множитель х).
– проще исходного (то, что cos x заменился на sin x не изменяет сути решения, а вместо х 2 появился более простой множитель х).
К интегралу I 1 – снова применим интегрирование по частям, полагая
| u = х | du = dx |
| dυ = sin xdx | 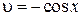 |
Это дает 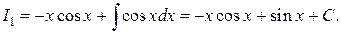
Заменяя I 1 найденным выражением, окончательно получим
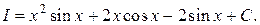
Практика показывает, что многократным интегрированием по частям можно найти интегралы следующих двух групп.
К первой группе относятся интегралы:
1. 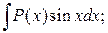 2.
2. 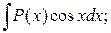 3.
3. 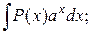 4.
4. 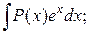
где Р (х) – многочлен некоторой степени, который и берется за функцию u. При многократном дифференцировании он «исчезает».
Ко второй группе относятся следующие интегралы:
1. 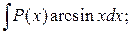 2.
2. 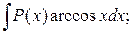 3.
3. 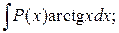 4.
4. 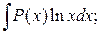
Здесь нужно избавится от трансцендентных функций arcsin x, arccos x, arctg x и ln x, поэтому ихпринимают за «u».
Пример 5. Вычислить 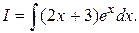 Так как интеграл из первой группы, то
Так как интеграл из первой группы, то
| u = 2 х + 3 | du = 2 dx |
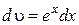 | 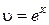 |
Применяя формулу интегрирования по частям, получим:
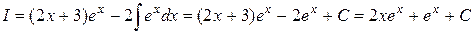
Пример 6. Найти 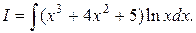 Интеграл второй группы, следовательно
Интеграл второй группы, следовательно 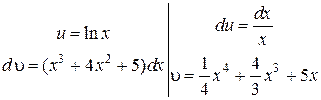
По формуле (1.3.1) находим
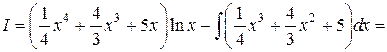
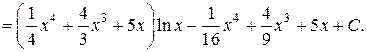
Повторное интегрирование по частям иногда приводит к первоначальному интегралу, и тогда получается или ничего не дающее тождество (был сделан неправильный выбор множителей u и d υ) или такое равенство, из которого удается найти выражение для искомого интеграла.
Пример 7. Вычислить интеграл 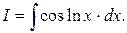 Подынтегральное выражение содержит единственную функцию cosln x, поэтому
Подынтегральное выражение содержит единственную функцию cosln x, поэтому
| u = cosln x | 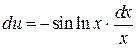 |
| dυ = dx | υ = x |
По формуле (1.3.1) получим 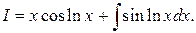 Ко второму интегралу еще раз применим интегрирование по частям
Ко второму интегралу еще раз применим интегрирование по частям
| u = sinln x | 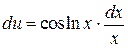 |
| dυ = dx | υ = x |
Тогда 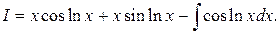
Двойное интегрирование по частям привело к исходному интегралу т.е.
I = x (cosln x + sinln x) – I.
Перенесем его в левую часть последнего равенства
2 I = x (cosln x + sinln x),
отсюда исходный интеграл будет равен
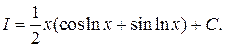
Таким же способом вычисляют интегралы 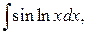
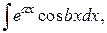
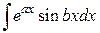 и некоторые другие, они получили название циклических. Последние два интеграла можно занести в таблицу интегралов. Для них найдены следующие формулы.
и некоторые другие, они получили название циклических. Последние два интеграла можно занести в таблицу интегралов. Для них найдены следующие формулы.
1. 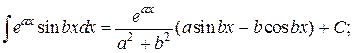
2. 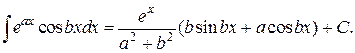
Пример 8. Найти 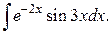 Здесь a = –2; b = 3, применяя первое равенство, получим
Здесь a = –2; b = 3, применяя первое равенство, получим
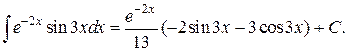
Задачи для самостоятельного решения. Вычислить
100. 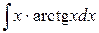 ; ; | 101. 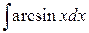 ; ; |
102. 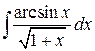 ; ; | 103. 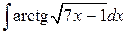 ; ; |
104. 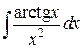 ; ; | 105. 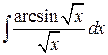 ; ; |
106. 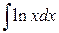 ; ; | 107. 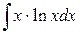 ; ; |
108. 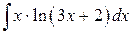 ; ; | 109. 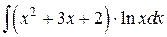 ; ; |
110. 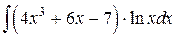 ; ; | 111. 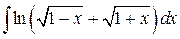 ; ; |
112. 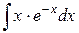 ; ; | 113. 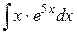 ; ; |
114. 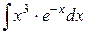 ; ; | 115. 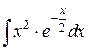 ; ; |
116. 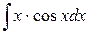 ; ; | 117. 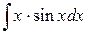 ; ; |
118. 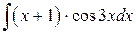 ; ; | 119. 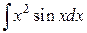 ; ; |
120. 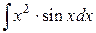 ; ; | 121.  ; ; |
122.  ; ; | 123. 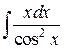 ; ; |
124. 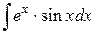 ; ; | 125. 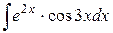 ; ; |
126. 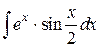 ; ; | 127. 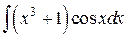 ; ; |
128.  ; ; | 129. 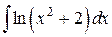 ; ; |
130. 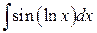 ; ; | 131. 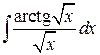 ; ; |
Практическое занятие 1.4. Многочлены и их свойства. Разложение на множители. Разложение рациональной функции на простейшие дроби
Сумму конечного числа степенных функций вида:
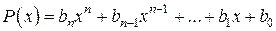 ,
,
где n -целое положительное число, называют многочленом степени n;
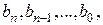 – коэффициенты многочлена, они могут быть как действительными, так и комплексными числами, причем
– коэффициенты многочлена, они могут быть как действительными, так и комплексными числами, причем 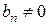 ,
,
х – независимая переменная, также может принимать действительные и комплексные значения. Степень многочлена определяет по старшей степени, входящих в него степенных функций.
Например 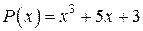 – многочлен третьей степени с действительными коэффициентами
– многочлен третьей степени с действительными коэффициентами 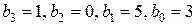 .
.
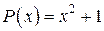 – многочлен второй степени с действительными коэффициентами.
– многочлен второй степени с действительными коэффициентами.
Числа: 3, 1, 2+ i – многочлены нулевой степени.
Многочлен тождественно равен нулю, если все его коэффициенты равны нулю.
Число 0 – является многочленом, степень которого неопределенна.
 2015-04-12
2015-04-12 14731
14731
