| Теория | Практика |
Чтобы разложить многочлен на множители нужно сгруппировать члены многочлена так, чтобы группы имели одинаковый общий множитель, записать сумму группировок и вынести общий множитель за скобки в каждой группе   x2+3x-4x-12=0 (x2+3x)+(-4x-12)=0 x(x+3)-4(x+3)=0 (x+3)(x-4)=0 x +3=0 или x-4=0 x=-3 x=4 Ответ: -3; 4 x=-3 x2+3x-4x-12=0 (x2+3x)+(-4x-12)=0 x(x+3)-4(x+3)=0 (x+3)(x-4)=0 x +3=0 или x-4=0 x=-3 x=4 Ответ: -3; 4 x=-3 | 1. Решите уравнение: 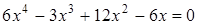 Решение. Решение. 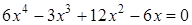 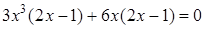 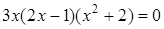 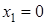 , , 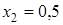 Ответ: 0; 0,5. 2. Решите уравнение: Ответ: 0; 0,5. 2. Решите уравнение: 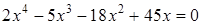 Решение: Решение: 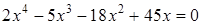 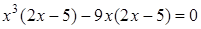 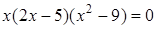 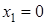 , , 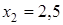 , , 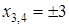 . Ответ: 0; 2,5; -3; 3. 3. Сократите дробь . Ответ: 0; 2,5; -3; 3. 3. Сократите дробь 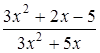 . Решение. Корни квадратного трехчлена . Решение. Корни квадратного трехчлена 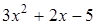 : : 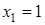 , , 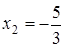 . Имеем: . Имеем: 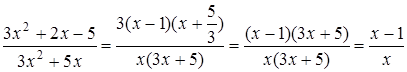 . Замечание. Можно разложить трехчлен на множители способом группировки: . Замечание. Можно разложить трехчлен на множители способом группировки: 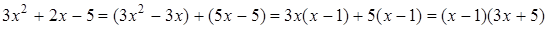 Ответ: Ответ: 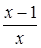 . 4. (Демо 2010, Задание 17) Решите уравнение . 4. (Демо 2010, Задание 17) Решите уравнение 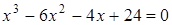 . Решение. Разложим на множители левую часть уравнения. Получим: . Решение. Разложим на множители левую часть уравнения. Получим: 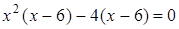 , , 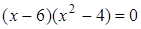 , , 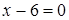 или или 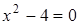 . Значит, уравнение имеет корни: -2; 2; 6. Ответ: -2; 2; 6. . Значит, уравнение имеет корни: -2; 2; 6. Ответ: -2; 2; 6. |
Реши сам:
1. Найдите произведение корней уравнения 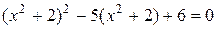 .
.
2. Решите уравнение 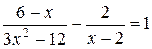 .
.
3. Найдите наибольший корень уравнения 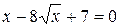 .
.
4. Докажите, что уравнение 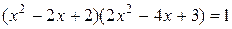 имеет корень равный 1, а других корней у него нет.
имеет корень равный 1, а других корней у него нет.
5. Найдите произведение корней уравнения 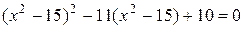 .
.
6. Решите уравнение 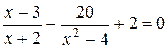 .
.
7. Найдите наименьший корень уравнения 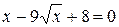 .
.
8. Докажите, что уравнение 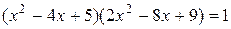 имеет корень равный 2, а других корней у него нет.
имеет корень равный 2, а других корней у него нет.
9. Найдите произведение корней уравнения 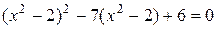 .
.
10. Решите уравнение 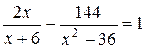 .
.
11. Найдите наибольший корень уравнения 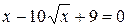 .
.
12. Докажите, что уравнение 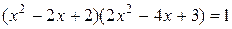 имеет корень равный 1, а других корней у него нет.
имеет корень равный 1, а других корней у него нет.
13. Разложите на множители: 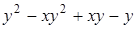 .
.
14. Решите уравнение 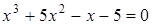 .
.
| Модель 1 Баллы | Критерии оценки выполнения задания |
| Ход решения верный, оба его шага выполнены, получен верный ответ. | |
| Ход решения правильный, многочлен в левой части уравнения разложен на множители, но при этом допущена ошибка в знаке, например, получен двучлен, ответ дан с учетом этой ошибки. 24 x + Или: допущена описка на последнем шаге. | |
| Другие случаи, не соответствующие указанным критериям. | |
| Модель 2 Баллы | Критерии оценки выполнения задания |
| Ход решения верный, оба его шага выполнены, получен верный ответ. | |
| Ход решения правильный, многочлен в левой части уравнения разложен на множители, но при этом допущена ошибка в знаке, например, получен двучлен, ответ дан с учетом этой ошибки. Или: допущена описка на последнем шаге. 24x+ | |
| Другие случаи, не соответствующие указанным критериям. |
 2015-04-12
2015-04-12 1693
1693
