2015-04-23
2436
Введение новых переменных может быть как явным, так и неявным. Классифицируем уравнения по способам неявной реализации метода замены переменной.
Использование основного свойства дроби. Данный прием применяется в уравнениях следующего вида:
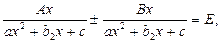
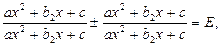
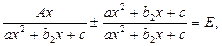где 
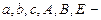постоянные, 
.
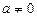В таких уравнениях сначала проверяют, является ли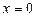 
корнем уравнения, и производят замену 
.
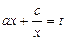Выделение полного квадрата. Выделение квадрата двучлена чаще всего встречается при решении уравнений, которые можно привести к такому виду, чтобы одна часть уравнения представляла собой сумму квадратов двучлена.
Переход к системе уравнений. Этот приём целесообразен при решении уравнений вида: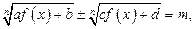 
где коэффициенты 
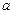и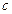 
равны, противоположны по знаку или отличаются на постоянный множитель.
Раскрытие скобок парами. Такой методдаёт хороший эффект в уравнениях вида: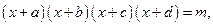 
где 
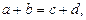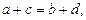или 
или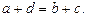 
Раскрытие скобок парами и деление обеих частей уравнения. Раскрытие скобок парами и деление обеих частей уравненияцелесообразно применять в случаях, когда перед нами уравнение вида:
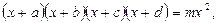где 
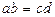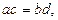, или 
или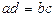 
.
Сведение к однородному уравнению. Преобразовав один из множителей и выделив из него выражение, равное второму множителю и подставляя полученное выражение в исходное уравнение, удаётся прийти к однородному уравнению второй степени, то есть к уравнению вида: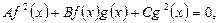 
где 
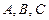‒ постоянные, отличные от нуля, а 
, 
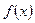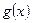‒ многочлены.
Тригонометрическая подстановка. Тригонометрическая подстановка используется в тех случаях, когда область определения исходного уравнения совпадает с областью значения тригонометрической функции или включается в эту область.
Приведем примеры типовых заданий, сводящихся к применению метода замены при решении уравнений.
Пример. Решим уравнение: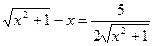 
.
Решение. Область определения уравнения – все действительные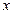 
.
Введем новую переменную. Пусть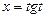 
, где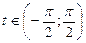 
.
Тогда исходное уравнение примет вид: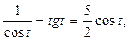 
(1)
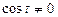, то уравнение (1)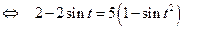 
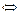
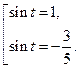
Из решения данных уравнений промежутку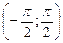 
принадлежат только 
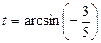. Поэтому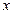 
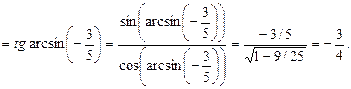
Ответ.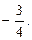 
Пример. Решим уравнение: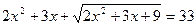 
.
Решение. Если в качестве новой переменной выбрать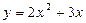 
уравнение упрощается, но остаётся иррациональным.
Более удобна замена: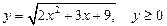 
.
Тогда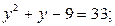 
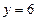или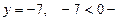 
посторонний корень.
Возвращаясь к исходной переменной, имеем:
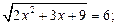
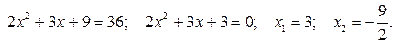
Ответ.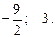 
Пример. Решим уравнение: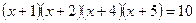 
Решение. К данному уравнению можно применить рассмотренный выше приём – «раскрытие скобок парами». Суммы чисел, стоящих в первой и четвёртой, во второй и третьей скобках, равны, то есть 1+5=2+4. Перемножим эти пары скобок, получим уравнение: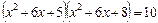 
.
Введем новую переменную. Пусть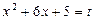 
, тогда: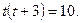 
Решив квадратное уравнение: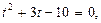 
находим, что 
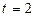или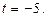 
Вернемся к исходной переменной и решим совокупность уравнений:
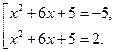
В первом уравнении совокупности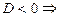 
корней нет.
Перепишем второе уравнение: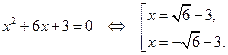 
Ответ.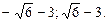 
Пример. Решим уравнение: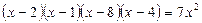 
.
Решение. Заметим, что произведение чисел, стоящих в первой и четвёртой, во второй и третьей скобках, равны, то есть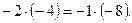 
Перемножим указанные пары скобок: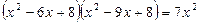 
.
Так как 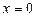не есть решение данного уравнения, то, разделив обе части на 
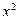, получим равносильное исходному уравнение: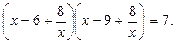 
Введем новую переменную. Пусть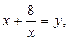 
тогда:
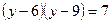
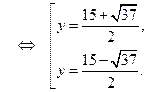
Вернемся к исходной переменной, имеем: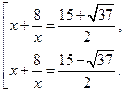 
Решения первого уравнения данной совокупности:
, 
.
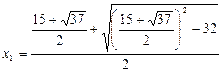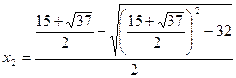Второе уравнение этой совокупности решений не имеет.
Ответ.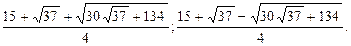 
Пример. Решим уравнение: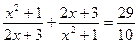 
.
Решение. Введем новую переменную. Пусть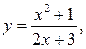 
тогда исходное уравнение примет вид: 
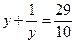. Поскольку 
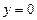не является корнем этого уравнения, то уравнение равносильно уравнению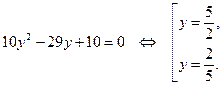 
Возвращаясь к исходной переменной, имеем:
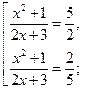
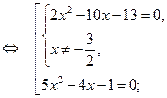
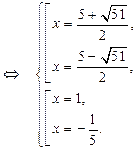
Ответ.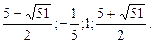 
Прежде, чем решить следующее уравнение, напомним алгоритм решения возвратного уравнения:
– разделить левую и правую части уравнения на 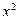. При этом не происходит потери решения, т. к. 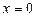не является корнем исходного уравнения при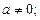 
– группировкой привести полученное уравнение к виду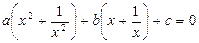 
– ввести новую переменную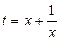 
, тогда выполнено 
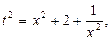то есть 
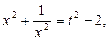в новых переменных рассматриваемое уравнение является квадратным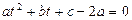 
– решить его относительно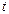 
, возвратиться к исходной переменной.
Пример. Решим уравнение: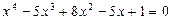 
.
Решение. Исходя из алгоритма решения таких уравнений, разделим левую и правую части уравнения на 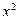, получим равносильное уравнение:
.
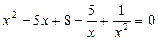Сгруппировав слагаемые, перепишем уравнение в виде: 
или в виде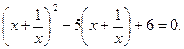 
Введем новую переменную. Пусть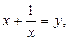 
тогда: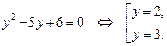 
Возвращаясь к исходной переменной, имеем: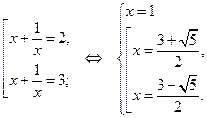 
Ответ.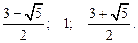 
Пример. Решим уравнение: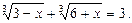 
Решение. Введем новые переменные. Пусть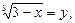 
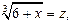тогда:
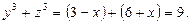
Таким образом, для переменных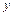 
и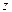 
имеем симметричную систему:
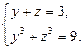
Обозначим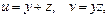 
тогда 
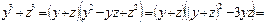
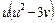
Таким образом,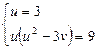 
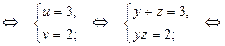
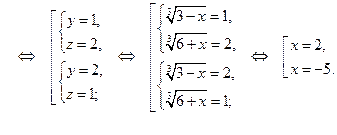
Ответ.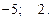 
Пример. Решим уравнение: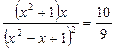 
.
Решение. Если в уравнении освободиться от знаменателя, провести все необходимые преобразования, то получим возвратное уравнение четвёртой степени. Однако, более рациональным является другой способ. Поделим числитель и знаменатель дроби, расположенной в левой части, на .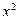
Получим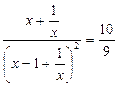 
. Введем новую переменную.
Пусть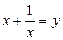 
, тогда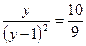 
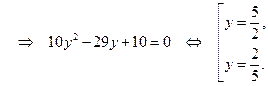
Обратная замена: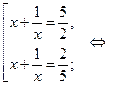 
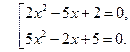
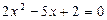или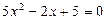 
; 
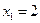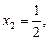
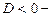корней нет.
Ответ.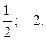 
Пример. Решим уравнение: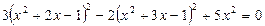 
.
Решение. Так как 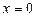не является корнем данного уравнения, то, разделив обе его части на 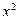, получим: 
.
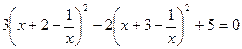Введем новую переменную.
Пусть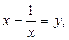 
тогда: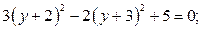 
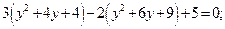
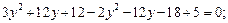
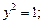
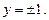
Вернёмся к исходной переменной, имеем: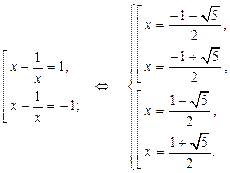 
Ответ.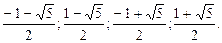 
Пример. Решим уравнение: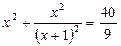 
.
Решение. Поскольку в левой части стоит сумма двух квадратов, целесообразно попытаться дополнить её до квадрата суммы или разности.
Во втором случае получим: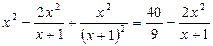 
;
; 
.
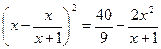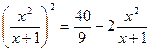Введем новую переменную. Пусть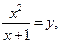 
тогда: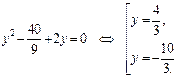 
Вернёмся к исходной переменной, имеем:
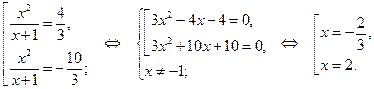
Ответ.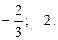 
Пример. Решим уравнение: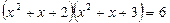 
.
Решение. Введем новую переменную. Пусть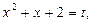 
тогда:
; 
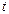
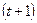
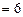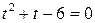
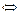
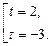
Обратная замена: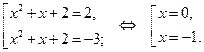 
Ответ.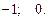 
Пример. Решим уравнение: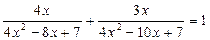 
.
Решение. Так как 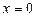не является решением уравнения, то, разделив числитель и знаменатель каждой дроби в левой части на 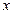, перепишем его в виде: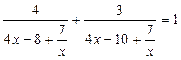 
Введем новую переменную. Пусть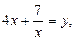 
тогда: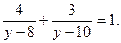 
Решения этого уравнения: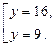 
Вернемся к исходной переменной, имеем: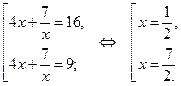 
Ответ.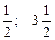 
.
Пример. Решим уравнение: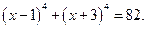 
Решение. Обозначим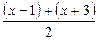 
через 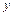, то есть введем новые переменные: 
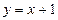или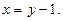 
Тогда первоначальное уравнение имеет вид: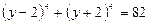 
, применим формулу 
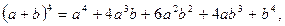имеем: 
.
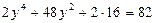Найдем корни квадратного уравнения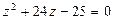 
: 
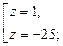
тогда решения биквадратного уравнения: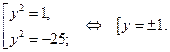 
Вернемся к исходной переменной.
Решения исходного уравнения: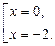 
Ответ.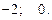 
Пример. Решим уравнение: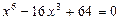 
.
Решение. Представим уравнение в виде: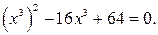 
Введем новую переменную. Пусть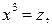 
тогда уравнение примет вид:
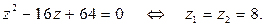
Вернемся к исходной переменной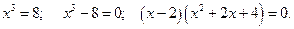 
Последнее уравнение равносильно совокупности уравнений:
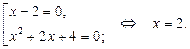Ответ.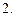 
Пример. Решим уравнение: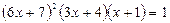 
.
Решение. Умножим обе части уравнения на 12. Введем новую переменную. Пусть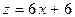 
, тогда получим уравнение 
.
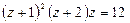Перепишем полученное уравнение в виде:
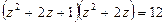. Пусть 
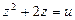, тогда: 
.
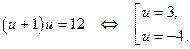Уравнение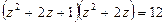 
.
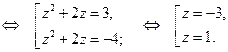Обратная замена: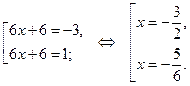 
Ответ.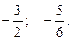 
Пример. Решим уравнение: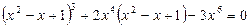 
.
Решение. Если раскрыть скобки и привести подобные, то получим уравнение пятой степени стандартного вида.
Если ввести новые переменные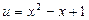 
и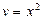 
, то получим уравнение 
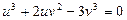, являющееся однородным уравнением степени 3 относительно 
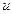и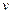 
.
Однородные уравнения относительно 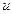и 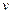обладают тем свойством, что если разделить все члены уравнения на наивысшую степень одной из переменных, например 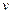, если 
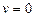не является корнем уравнения, то оно превращается в уравнение с одной переменной 
.
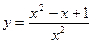Решим уравнение: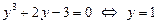 
.
Разделим многочлен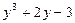 
на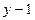 
, перейдём к равносильному уравнению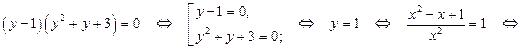 
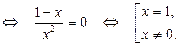
Ответ.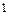 
.
Вывод по II главе:
привели методы решения некоторых систем и совокупностей уравнений,
Во второй главе мы рассмотрели некоторые приемы преобразования систем уравнений и некоторые методы решения систем и совокупностей уравнений с одной, двумя и с тремя переменными, подробно изучили графический метод решения уравнений.. Разработали систему практических заданий, иллюстрирующих теоретические положения.
В приложении мы привели задания повышенной сложности. Подобрали практические задания, иллюстрирующие теоретические положения раздела «Уравнения».
Структура изложения теоретического материала определена целью − способствовать формированию у будущего учителя четкой системы понятий и практического использования этих понятий в процессе преподавания начального курса математики. Практические задания могут с успехом применяться как в учебном процессе, так и для самостоятельной работы студентов.
