1. 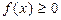 , так как функция распределения является неубывающей.
, так как функция распределения является неубывающей.
2. 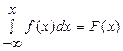 (следствие из определения f(x))
(следствие из определения f(x))
3. 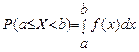 ,
,
Действительно, 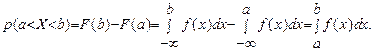
4. 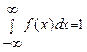 (условие нормировки),
(условие нормировки),
если же возможные значения случайной величины принадлежат отрезку [ a, b ],
т.е. f(x)= 0 при x < a и x > b то 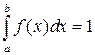
5. 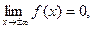 так как
так как 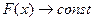 при
при 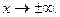
Пример 1. Плотность распределения непрерывной случайной величины задана формулой
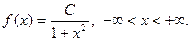
Найти: а) значение константы С; б) вид функции распределения; в) p (-1 < x < 1).
Решение. а) значение константы С найдем из свойства 4:
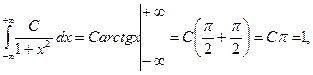 откуда
откуда 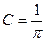 .
.
б) 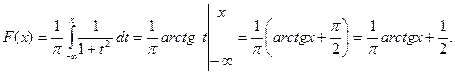
в) 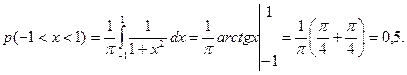
Пример 2. Функция распределения непрерывной случайной величины имеет вид:
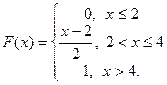
Найти плотность распределения.
Решение.
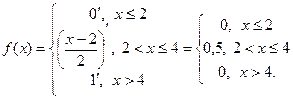
 2015-04-12
2015-04-12 506
506








