Непрерывная случайная величина называется распределенной по нормальному закону, если ее плотность распределения имеет вид:
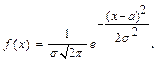 (24.1)
(24.1)
где а и σ - параметры.
График плотности нормального распределения называют нормальной кривой (кривой Гаусса). Исследуем функцию (24.1).
1) Область определения этой функции: (-∞, +∞).
2) f (x) > 0 при любом х (следовательно, весь график расположен выше оси О х).
3) 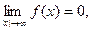 то есть ось О х служит горизонтальной асимптотой графика при
то есть ось О х служит горизонтальной асимптотой графика при 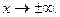
4) 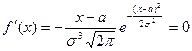 при х = а;
при х = а; 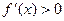 при x > a,
при x > a, 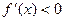 при x < a. Следовательно,
при x < a. Следовательно, 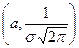 - точка максимума.
- точка максимума.
5) F (x – a) = f (a – x), то есть график симметричен относительно прямой х = а.
6) 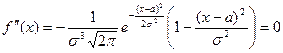 при
при 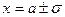 , то есть точки
, то есть точки 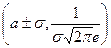 являются точками перегиба.
являются точками перегиба.
Для вычисления математического ожидания нормально распределенной случайной величины воспользуемся тем, что интеграл Пуассона 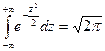 .
.
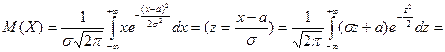
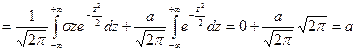 (первое слагаемое равно 0, так как подынтегральная функция нечетна, а пределы интегрирования симметричны относительно нуля).
(первое слагаемое равно 0, так как подынтегральная функция нечетна, а пределы интегрирования симметричны относительно нуля).
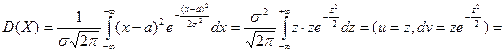
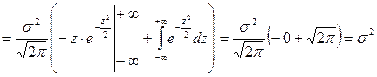 .
.
Следовательно, параметры нормального распределения (а и σ) равны соответственно математическому ожиданию и среднему квадратическому отклонению данной случайной величины.
Примерный вид кривых Гаусса для различных значений параметров показан на рисунке
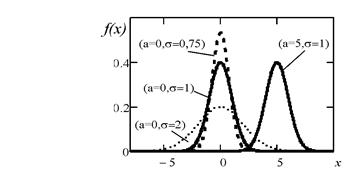
Найдем вид функции распределения для нормального закона:
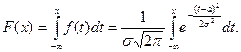 (24.2)
(24.2)
Интеграл в (24.2) невозможно выразить через элементарные функции. Поэтому для вычисления значений F (x) приходится пользоваться таблицами. Они составлены для случая, когда а = 0, а σ = 1(нормированное распределение), то есть для функции
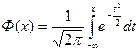 (24.3)
(24.3)
называемой функцией Лапласа.
Функцию распределения для нормально распределённой случайной величины при произвольных значениях параметров можно выразить через функцию Лапласа, если сделать замену: 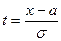 , тогда
, тогда 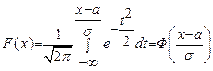 . (24.4)
. (24.4)
А вероятность попадания нормально распределенной случайной величины на заданный интервал:
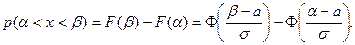 (24.5)
(24.5)
Замечание. Если используется затабулированная функция Лапласа вида 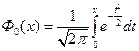 , то следует учитывать, что
, то следует учитывать, что 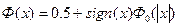 .
.
Пример. Случайная величина Х имеет нормальное распределение с параметрами а = 3, σ = 2. Найти вероятность того, что она примет значение из интервала (4, 8).
Решение.
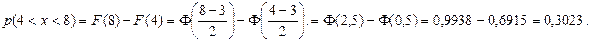
 2015-04-12
2015-04-12 649
649








