Распространим определения числовых характеристик случайных величин на непрерывные случайные величины. При этом 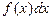 , будем рассматривать как вероятность того, что случайная величина примет значение лежащее в бесконечно малом интервале
, будем рассматривать как вероятность того, что случайная величина примет значение лежащее в бесконечно малом интервале 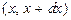 .
.
Математическое ожидание непрерывной случайной величины равно
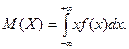 (22.1)
(22.1)
Общее определение дисперсии сохраняется для непрерывной случайной величины таким же, как и для дискретной (17.2), а вычислена дисперсия может по формуле:
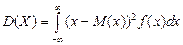 (22.2)
(22.2)
или 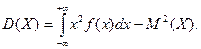 (22.3)
(22.3)
Среднее квадратическое отклонение вычисляется по формуле (17.6): 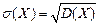 .
.
Замечание. Если все возможные значения непрерывной случайной величины не выходят за пределы интервала [ a, b ], то интегралы в формулах (22.1) - (22.3) вычисляются в пределах интервала [ a, b ].
Пример. Плотность распределения случайной величины Х имеет вид:
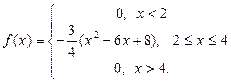
Найти М (Х), D (X), σ.
Решение. 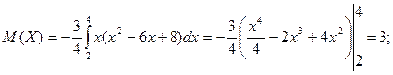
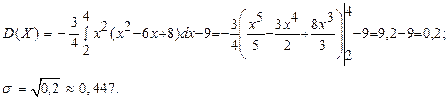
 2015-04-12
2015-04-12 385
385








