Правило «трех сигм»

Найдем вероятность того, что нормально распределенная случайная величина примет значение из интервала (а - 3 σ, а + 3 σ):

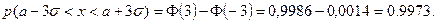
Следовательно, вероятность того, что значение случайной величины окажется вне этого интервала, равна 0,0027, то есть составляет 0,27% и может считаться пренебрежимо малой. Таким образом, на практике можно считать, что все возможные значения нормально распределенной случайной величины лежат в интервале (а - 3 σ, а + 3 σ).

Полученный результат позволяет сформулировать правило «трех сигм»: если случайная величина распределена нормально, то модуль ее отклонения от х = а не превосходит 3σ.