1. Постройте график функции и перечислите ее свойства:
а) 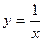 ,
,
б) 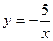 .
.
2. Начертите график какой-либо функции с областью определения [-3;4] так,
чтобы эта функция:
а) возрастала в промежутке [-3;0] и убывала в промежутке [0;4];
б) убывала в промежутке [-3;1] и возрастала в промежутке [1;4].
Квадратичная функция
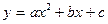 , где
, где 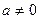
график – парабола
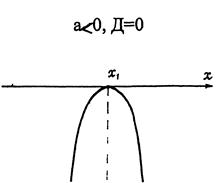
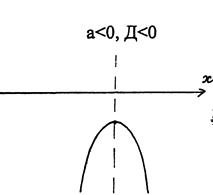
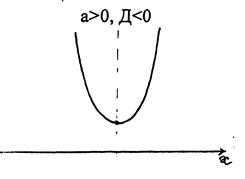
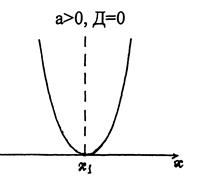
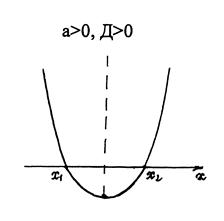
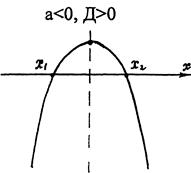
Различные представления квадратичной функции:
1. Выделение полного квадрата
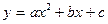
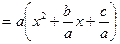
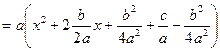
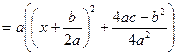 =
=
= 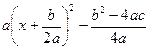
2. Разложение на линейные множители:
при 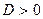
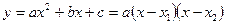 ,
,
при 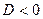
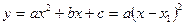 ,
,
при 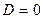 разложить на множители нельзя.
разложить на множители нельзя.
Свойства квадратичной функции
− Область определения: 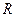
− Область значений:
при 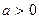
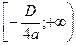 ,
,
при 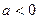
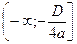 .
.
− Четность, нечетность:
при  функция четная,
функция четная,
при 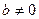 функция не является ни четной, ни нечетной.
функция не является ни четной, ни нечетной.
− Нули:
при 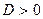 два нуля:
два нуля: 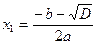 ,
, 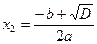 ;
;
при 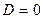 один нуль:
один нуль: 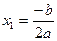 ;
;
при 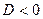 нулей нет.
нулей нет.
− Промежутки знакоостоянства:
если 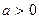 ,
, 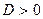 , то
, то 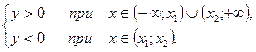
если 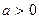 ,
, 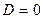 , то
, то 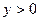 при
при 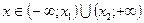 ,
,
если 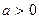 ,
, 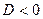 , то
, то 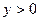 при
при 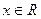
если 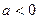 ,
, 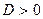 , то
, то 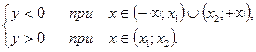
если 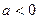 ,
, 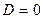 , то
, то 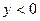 при
при 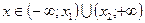
если 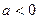 ,
, 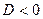 , то
, то 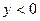 при
при 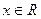
− Промежутки монотонности:
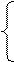 при
при 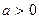 функция возрастает при
функция возрастает при 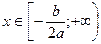
Функция убывает при 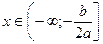
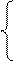 при
при 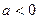 функция возрастает при
функция возрастает при 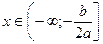
Функция убывает при 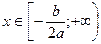
− Экстремумы:
при 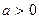
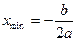 ,
, 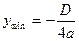
при 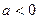
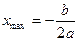 ,
, 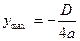
Направление ветвей, характерные точки и ось симметрии параболы, являющейся графиком функции у = ах2 + вх + с
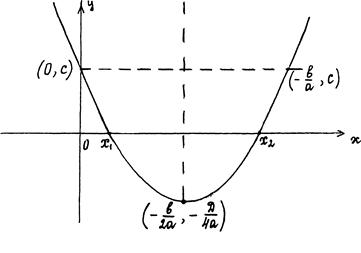
− Направление ветвей параболы:
при 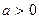 ветви направлены вверх,
ветви направлены вверх,
при 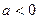 ветви направлены вниз.
ветви направлены вниз.
− Координаты вершины параболы: 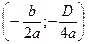 .
.
− Ось симметрии параболы – прямая 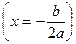 .
.
− Точки пересечения (касания) графика с осью 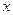 :
:
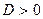
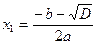 ,
, 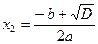 (точки пересечения)
(точки пересечения)
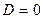
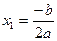 (точка касания)
(точка касания)
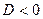 общих точек у графика с осью
общих точек у графика с осью 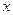 нет.
нет.
− Точка пересечения графика с осью 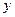 :
: 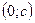 ,
,
симметричная ей точка относительно оси параболы 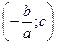 .
.
 2015-04-12
2015-04-12 606
606








