2015-04-12
1564
Вопросы для подготовки к коллоквиуму
1. n -мерный вектор. Определение, линейные преобразования.
2. n -мерное векторное пространство. Определение, линейные (не)зависимые вектора.
3. Размерность векторного пространства. Базис. Координаты вектора в базисе.
4. Евклидово пространство. Определение, свойства, длина вектора.
7. Смешанное произведение векторов.
8. Двойное векторное произведение.
9. Линейные операторы. Определение, свойства, действия над линейными операторами.
10. Собственные векторы и собственные значения линейного оператора.
Задания для аудиторной самостоятельной работы
1. На плоскости относительно некоторого базиса даны координаты трех векторов: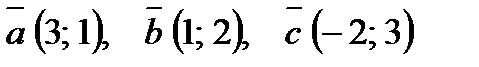 
;
1) Найти координаты векторов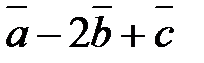 
; 
.
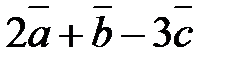2) Проверить, что векторы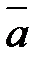 
и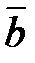 
образуют базис на плоскости. Найти координаты вектора 
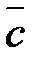в этом базисе.
3) Определить при каком значении параметра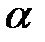 
векторы 
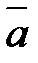и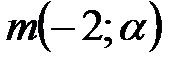 
будут коллинеарными.
4) Найти координаты вектора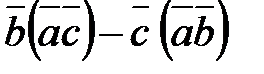 
.
5) Вычислить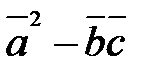 
, 
.
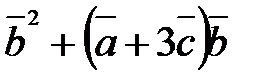6) Найти косинус угла между векторам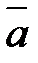и 
и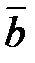 
.
2. В пространстве относительно некоторого базиса даны координаты трех векторов: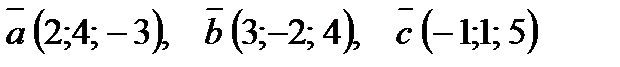 
.
1) Найти координаты векторов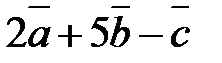 
, 
.
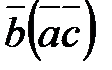2) Вычислить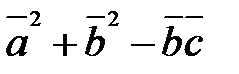 
; 
.
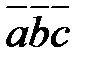3) Найти косинус угла между векторам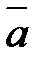и 
и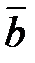 
.
3. На плоскости относительно декартовой системы координат даны координаты трех точек: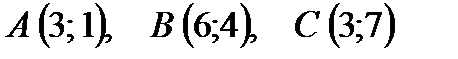 
;
Найти:
- Координаты вектора
.
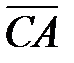2. Координаты точек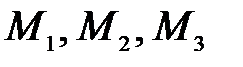 
, делящих отрезки 
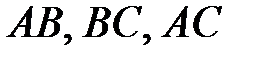в отношениях 
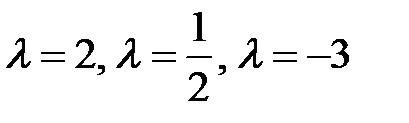, соответственно.
- Площадь треугольника
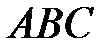. - Угол
.
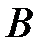Индивидуальное домашнее задание
Задание № 1. Даны векторы а =α m +β n и b =γ m +δ n, где | m |=k, | n |= l, (m,^n)=φ.
Найти: 1) (λ а +μ b)*(ν а +τ b); 2). пр b (ν а +τ b); 3). Cos(a,^ τ b).
| № вар. | α | β | γ | δ | ķ | l | φ | λ | μ | ν | τ |
| -5 | -4 | 5π/3 | -2 | 1/3 | |||||||
| -2 | -1 | π | -2 | ||||||||
| -2 | -3 | -1 | 4π/3 | -1 | |||||||
| -6 | -4 | 5π/3 | -1 | 1/2 | |||||||
| -2 | -4 | π/3 | -3 | ||||||||
| -5 | -3 | 2π/3 | -4 | ||||||||
| -4 | -2 | 4π/3 | -3 | -1/2 | |||||||
| -4 | π | -2 | -4 | ||||||||
| -3 | -2 | 4π/3 | -1 | ||||||||
| -3 | 2π/3 | -1/2 | |||||||||
| -2 | -6 | 5π/3 | -1/3 | ||||||||
| -2 | -4 | 7π/3 | -1/2 | ||||||||
| -1 | 3π/2 | -3 | |||||||||
| -2 | 2π | -3 | |||||||||
| -3 | 4π/3 | -3 | -1 | ||||||||
| -5 | π | -3 | 1/2 | -1 | |||||||
| -2 | π/2 | -2 | |||||||||
| -3 | 5π/3 | -1/2 | |||||||||
| -5 | -1 | 2π/3 | -5 | ||||||||
| -5 | -2 | 3π/2 | -2 | ||||||||
| -5 | -6 | π | -2 | ||||||||
| -7 | π/3 | -1 | |||||||||
| -6 | 2π/3 | -1/2 | |||||||||
| -5 | -7 | -3 | 3π/2 | -3 | -1 | ||||||
| -8 | -2 | 4π/3 | -3 | ||||||||
| -3 | 5π/3 | -2 | -2 | ||||||||
| -3 | -6 | π | -3 | -1 | |||||||
| -7 | -1 | -3 | 4π/3 | -2 | |||||||
| -4 | -2 | 5π/3 | -2 | -1/2 | |||||||
| -3 | -2 | π/3 | -1/2 |
Задание № 2. По координатам точек А, В, С для указанных векторов найти:
1). Модуль вектора а; 2). Скалярное произведение векторов а и b; 3).проекцию вектора с на d; 4). Координаты точки М, делящей отрезок l в отношении α:β.
| № | А | В | С | а= | b= | c= | d= | l | α | β |
| (4,6,3) | (-5,2,6) | (4,-4,-3) | 4CB-AC | AB | CB | AC | AB | |||
| (4,3,-2) | (-3,-1,4) | (2,2,1) | -5AC+2BC | AB | AC | BC | BC | |||
| (-2,-2,4) | (1,3,-2) | (1,4,2) | 2AC-3BA | BC | BC | AC | BA | |||
| (2,4,3) | (3,1,- 4) | (-1,2,2) | 2AB+4AC | BA | b | AC | BA | |||
| (2,4,5) | (1,-2,3) | (-1,-2,4) | 3AB-4AC | BC | b | AB | AB | |||
| (-1,-2,4) | (-1,3,5) | (1,4,2) | 3AC-7BC | AB | b | AC | AC | |||
| (1,3,2) | (-2,4,-1) | (1,3,-2) | 2AB+5CB | AC | b | AB | AB | |||
| (2,-4,3) | (-3,-2,4) | (0,0,-2) | 3AC- 4CB | c | AB | CB | AC | |||
| (3,4,- 4) | (-2,1,2) | (2,-3,1) | 5CB+4AC | c | BA | AC | BA | |||
| (0,2,5) | (2,-3,4) | (3,2,-5) | -3AB+4CB | c | AC | AB | AC | |||
| (-2,-3,-4) | (2,- 4,0) | (1,4,5) | 4AC- 8BC | c | AB | BC | AB | |||
| (-2,-3,-2) | (1,4,2) | (1,-3,3) | 2AC- 4BC | c | AB | AC | BC | |||
| (5,6,1) | (-2,4,-1) | (3,-3,3) | 3AB- 4BC | c | AC | AB | BC | |||
| (10,6,3) | (-2,4,5) | (3,-4,-6) | 5AC-2CB | c | BA | AC | CB | |||
| (3,2,4) | (-2,1,3) | (2,-2,-1) | 4BC-3AC | BA | AC | BC | AC | |||
| (-2,3,- 4) | (3,-1,2) | (4,2,4) | 7AC+4CB | c | AB | CB | AB | |||
| (4,5,3) | (- 4,2,3) | (5,-6,-2) | 9AB- 4BC | c | AC | AB | BC | |||
| (2,4,6) | (-3,5,1) | (4,-5,-4) | -6BC+2BA | c | CA | BA | BC | |||
| (-4,-2,-5) | (3,7,2) | (4,6,-3) | 9BA+3BC | c | AC | BC | BA | |||
| (5,4,4) | (-5,2,3) | (4,2,-5) | 11AC-6AB | BC | AB | AC | BC | |||
| (3,4,6) | (-4,6,4) | (5,-2,-3) | -7BC+4CA | BA | CA | BC | BA | |||
| (-5,-2,-6) | (3,4,5) | (2,-5,4) | 8AC-5BC | c | AB | BC | AC | |||
| (3,4,1) | (5,-2,6) | (4,2,-7) | -7AC+5AB | c | BC | AC | AB | |||
| (4,3,2) | (-4,-3,5) | (6,4,-3) | 8AC-5BC | c | BA | AC | BC | |||
| (-5,4,3) | (4,5,2) | (2,7,- 4) | 3BC+2AB | c | CA | AB | BC | |||
| (6,4,5) | (-7,1,8) | (2,-2,-7) | 5CB-2AC | AB | CB | AC | AB | |||
| (6,5,- 4) | (-5,-2,2) | (3,3,2) | 6AB-3BC | c | AC | CB | BC | |||
| (-3,-5,-6) | (3,5,- 4) | (2,6,4) | 4AC-5BA | CB | BA | AC | BA | |||
| (3,5,4) | (4,2,-3) | (-2,4,7) | 3AB- 4AC | AB | BA | AC | BA | |||
| (4,6,7) | (2,- 4,1) | (-3,-4,2) | 5AB-2AC | c | BC | AB | AB |
Задание № 3.
Доказать, что векторы а, b, c образуют базис, и найти координатывектора d в этом базисе.
| № варианта | a | b | c | d |
| (5,4,1) | (-3,5,2) | (2,-1,3) | (7,23,4) | |
| (2,-1,4) | (-3,0,-2) | (4,5,-3) | (0,11,-14) | |
| (-1,1,2) | (2,-3,-5) | (-6,3,-1) | (28,-19,-7) | |
| (1,3,4) | (-2,5,0) | (3,-2,-4) | (13,-5,-4) | |
| (1,-1,1) | (-5,-3,1) | (2,-1,0) | (-15,-10,5) | |
| (3,1,2,) | (-7,-2,-4) | (-4,0,3) | (16,6,15) | |
| (-3,0,1) | (2,7,-3) | (-4,3,5) | (-16,33,13) | |
| (5,1,2) | (-2,1,-3) | (4,-3,5) | (15,-15,24) | |
| (0,2,-3) | (4,-3,-2) | (-5,-4,0) | (-19,-5,-4) | |
| (3,-1,2) | (-2,3,1) | (4,-5,-3) | (-3,2,-3) | |
| (5,3,1) | (-1,2,-3) | (3,-4,2) | (-9,34,-20) | |
| (3,1,-3) | (-2,4,1) | (1,-2,5) | (1,12,-2j) | |
| (6,1,-3) | (-3,2,1) | (-1,-3,4) | (15,6,-17) | |
| (4,2,3) | (-3,1,-8) | (2,-4,5) | (-12,14,-31) | |
| (-2,1,3) | (3,-6,2) | (-5,-3,-1) | (31,-6,22) | |
| (1,3,6) | (-3,4,-5) | (1,-7,2) | (-2,17,5) | |
| (7,2,1) | (5,1,-2) | (-3,4,5) | (26,11,1) | |
| (3,5,4) | (-2,7,-5) | (6,-2,1) | (6,-9,22) | |
| (5,3,2) | (2,-5,1) | (-7,4,-3) | (36,1,15) | |
| (11,1,2) | (-3,3,4) | (-4,-2,7) | (-5,11,-15) | |
| (9,5,3) | (-3,2,1) | (4,-7,4) | (-10,-13,8) | |
| (7,2,1) | (3,-5,6) | (-4,3,-4) | (-1,18,-16) | |
| (1,2,3) | (-5,3,-1) | (-6,4,5) | (-4,11,20) | |
| (-2,5,1) | (3,2,-7) | (4,-3,2) | (-4,22,-13) | |
| (3,1,2) | (-4,3,-1) | (2,3,4) | (14,14,20) | |
| (3,-1,2) | (-2,4,1) | (4,-5,-1) | (-5,11,1) | |
| (4,5,1) | (1,3,1) | (-3,-6,7) | (19,33,0) | |
| (1,-3,1) | (-2,-4,3) | (0,-2,3) | (-8,10,13) | |
| (5,7,-2) | (-3,1,3) | (1,-4,6) | (14,9,-1) | |
| (-1,4,3) | (3,2,-4) | (-2,-7,1) | (6,20,-3) |
Задание № 4.
Выяснить являются ли следующие векторы линейно зависимыми:
| № варианта | Х1= | Х2= | Х3= | Х4= |
| (-3,1,5) | (6,-2,15) | |||
| (4,-12,28) | (-7,21,-49) | |||
| (1,2,3,0) | (2,4,6,1) | |||
| (1,2,3) | (2,5,7) | |||
| (1,2,3) | (2,5,7) | (3,7,11) | ||
| (1,4,7,10) | (2,5,8,11) | (3,6,9,12) | ||
| (1,2,3) | (4,5,6) | (7,8,9) | ||
| (4,5,6,) | (7,8,9) | (10,11,12) | ||
| (1,1,1) | (1,0,-1) | (1,3,5) | ||
| (1,2,-1,-2) | (-2,-3,0,1) | (1,2,1,4) | ||
| (2,3,0,-1) | (1,2,1,4) | (1,3,-1,0) | ||
| (1,3,5) | (2,7,3) | (3,9,4) | ||
| (1,2,1,1) | (2,3,1,0) | (3,1,1,-2) | (4,2,-1,-6) | |
| (1,2,-1,-2) | (7,14,-1,2) | (1,3,-1,0) | (2,3,0,-1) | |
| (2,9,3,5) | (1,2,2,-1) | (2,3,2,5) | (-1,4,3,-1) | |
| (1,2,1,1) | (0,4,1,3) | (2,3,1,0) | (3,1,1,-2) | |
| (1,1,1,1) | (1,1,-1,-1) | (1,-1,1,-1) | (1,-1,-1,1) | |
| (4,3,-1,1) | (2,1,-3,2) | (1,-3,0,1) | (1,5,2,-2) | |
| (2,2,7,-1) | (3,-1,2,4) | (1,1,3,1) | ||
| (3,2,-5,4) | (3,-1,3,-3) | (3,5,-13,11) | ||
| (2,3,-4,-1) | (1,-2,1,3) | (5,-3,-1,8) | (3,8,-9,-5) | |
| (2,-1,1,1) | (1,2,1,-1) | (1,1,2,1) | ||
| (2,1,-3) | (3,1,-5) | (4,2,-1) | ||
| (1,1,1,1) | (1,1,-1,-1) | (1,1,1,-1) | (1,-1,-1,1) | |
| (1,2,1,0) | (-1,1,1,1) | (2,-1,0,-1) | (1,-1,3,7) | |
| (2,1,3,1) | (1,2,0,1) | (-1,1,-3,0) | ||
| (2,1,3,-1) | (-1,1,-3,1) | (4,5,3,-1) | (1,5,-3,1) | |
| (1,2,-1,-2) | (3,1,1,1) | (-1,0,1,-1) | ||
| (2,-1,2,3) | (-1,1,1,-2) | (1,-2,-5,1) | (1,2,11,-1) | |
| (2,-1,1,1) | (-1,1,-2,2) | (2,1,-5,11) | (1,3,-1,0) |
