Тема 12 Функции нескольких переменных
До сих пор мы говорили о функции одной переменной 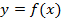 , где х – независимая переменная или аргумент. В задачах естествознания часто какой то показатель, например точечная температура тела (Т), может зависеть от нескольких независимых переменных, в данном случае
, где х – независимая переменная или аргумент. В задачах естествознания часто какой то показатель, например точечная температура тела (Т), может зависеть от нескольких независимых переменных, в данном случае 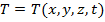 , где
, где 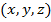 - координаты точки пространства, t – время, то есть имеем функцию четырех независимых переменных.
- координаты точки пространства, t – время, то есть имеем функцию четырех независимых переменных.
Объем цилиндра 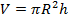 является функцией двух независимых переменных: R – радиуса и h – высоты цилиндра.
является функцией двух независимых переменных: R – радиуса и h – высоты цилиндра.
Евклидова плоскость и евклидово пространство
Множество всех упорядоченных пар вещественных чисел 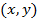 называют координатной плоскостью и каждая точка на ней характеризуется парой своих координат
называют координатной плоскостью и каждая точка на ней характеризуется парой своих координат 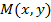 .
.
Координатная плоскость называется евклидовой плоскостью, если расстояние между любыми двумя точками 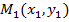 и
и 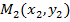 определяется формулой:
определяется формулой:
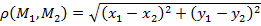 . (1)
. (1)
Аналогично вводится понятие евклидова трехмерного и, обобщенно, n – мерного пространства. В случае 3 – мерного пространства, расстояние между любыми точками 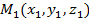 и
и 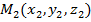 определяется формулой:
определяется формулой:
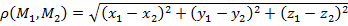 . (2)
. (2)
В случае n – мерного пространства расстояние между точками 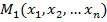 и
и 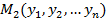 определяется:
определяется:
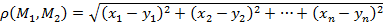 . (3)
. (3)
Для n – мерного евклидова пространства принято обозначение 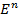 .
.
Примером подмножества пространства 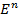 является n – мерный шар радиуса R с центром в точке
является n – мерный шар радиуса R с центром в точке 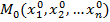 , который представляет собой множество точек
, который представляет собой множество точек 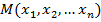 , координаты которых удовлетворяют неравенству:
, координаты которых удовлетворяют неравенству:
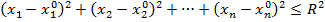 (4)
(4)
В двумерном случае, это – круг радиуса R:
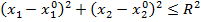 .
.
С учетом равенства (3), неравенство (4), характеризующее формулу n – мерного шара, можно представить в виде:
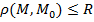 ,
,
что называют также R – окрестностью точки 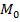 .
.
 2015-08-12
2015-08-12 5757
5757