Неравенство Коши-Буняковского.
Скалярным произведением векторов х,у принадлеж. R n: x=(x1,…,xn), y=(y1,…yn) называется число (х,у)= 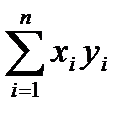
Для любых двух векторов а и b в евклидовом пространстве справедливо неравенство

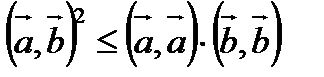
Доказательство:
Возьмем произвольное число t и составим вектор 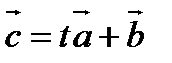
Тогда 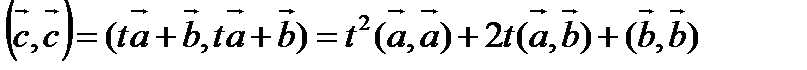
Легко заметить квадратный трехчлен, если 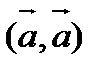 =α,
=α, 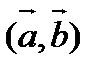 =β, а
=β, а 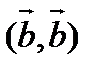 =γ, т.е.
=γ, т.е.
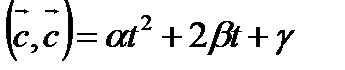
Квадратный трехчлен 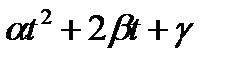 при любом значении t неотрицателен, поскольку
при любом значении t неотрицателен, поскольку 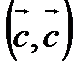 ≥0, следовательно, дискриминант данного трехчлена неположителен.
≥0, следовательно, дискриминант данного трехчлена неположителен.
D= β2- α γ≤ 0, подставим обратно выражения в неравенство:
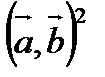 -
- 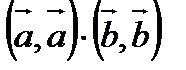 ≤0, или
≤0, или 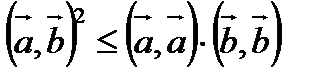 , чтд.
, чтд.
Т.о., нер-во Коши-Буняковского равносильно неравенству 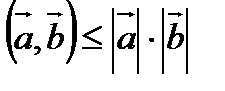
Неравенство треугольника.
Для любых двух векторов а и b в евклидовом пространстве справедливо соотношение, называемое неравенством треугольника:
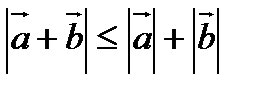
Доказательство:
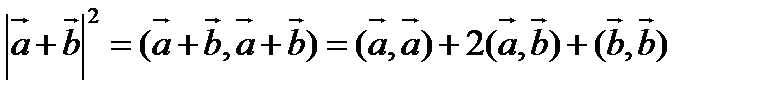
В силу неравенства Коши-Буняковского, согласно которому 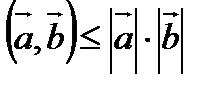 ,
,
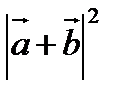
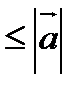 2+2
2+2 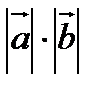 +
+ 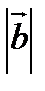 2=(
2=( +
+ 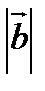 )2
)2
Извлечем корень из обеих частей этого неравенства без потери знака, т.к. обе части заведомо положительны.
Получим: 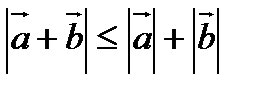
 2015-04-12
2015-04-12 1900
1900