Определение евклидова пр-ва. Норма вектора. Неравенство Коши-Буняковского и нер-во треугольника. Угол между двумя векторами

Определение. Действит. ли. пр-во V наз-ся Евклидовым пр-ом, если в нём любыми эл-ам x, y∈V поставл. в соответствие действит. число (x, y), назыв-ое скалярным произведением элементов x и y. При этом выполн. след. условия:

∀x, y, z∈V и ∀λ∈ℝ; (аксиомы).

1) (x, y)=(y, x);

2) (x, y, z)=(x, z)+(y, z);

3) (λx, y)= λ(x, y);

4) ∀x∈V, x≠0;(x, x)=0.

Определение. Пусть ε – евклидово пр-во, нормой вект. x∈ε наз-ся число, равное .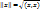

Св-ва нормы:

1°∀x∈ε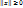

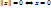
Док-во:

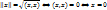
2° ∀x∈ε, ∀λ∈ ℝ; .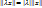

3° Нер-во Коши-Буняковского

∀x, y ∈ε: 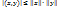или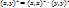

Док-во:

Пусть t – произв. линейн. число:

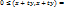
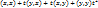
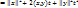
Рассмотрим квадратн. трехчлен:

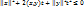, при любом t.

Значит 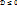, т.е.. 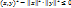. Откуда 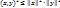. Ч.т.д.

4° Нер-во треугольника:

∀x, y∈ε: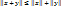

Док-во:

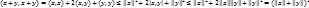
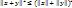
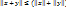
Определение. Пусть x и y (x≠0, y≠0)∈ε. Углом между величинами x и y наз-ся число, равное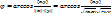

Определение корректно, если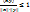

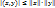→ Нер-во Коши-Буняковского.