Ортонормированные базисы (ОНБ) евклидова пр-ва. Теорема о существовании ОНБ, процесс ортогонализации Шмидта

Определение. Векторы x и y ∈ε наз-ся ортогональными (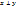), если (x, y)=0. Сист. векторов пр-ва ε наз-ся ортогональн., если все вектора этой сист. попарно ортогональны.

Теорема

Всякая ортогональная сист. ненулевых векторов лин. независима.

Док-во

x₁, …, x_n∈ε, ∀_ij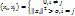

∀_ij=1, …, m; Пусть α₁x₁+…+α_mx_m=0

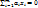; ∀k=1, …, m: x_k(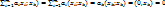

Т.к..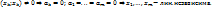

Определение. Сист. векторов 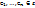назыв. ортогонализированной, если ∀_ij=1, …, m: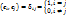

Определение. Упорядоченной сист. векторов 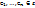наз-ся ОНБ пр-ва ε, если выполняется:

1) Система 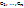– ортонормирована.

2) 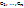– базис пр-ва ε.

Следствие

В n – мерном евклид. пр-ва любая упорядоченная ортонормированная система векторов образует ОНБ.