Пусть f1, …, fm лин. незав. сист. векторов в ε L{f1, …, fm} – лин. оболочка векторов, тогда в L{f1, …, fm} существ. ОНБ.
Док-во
L{f1, …, fm} – лин. подпр-во ε→ L{f1, …, fm} евклид. пр-во размерности m, где f1, …, fm обратн. базис.
Док-во индукции по m:
1) m=1, f1≠0, L{f1}
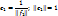
e1 – ОНБ в L{f1}
2) Допустим, что в L{f1, …, fm} ∃ ОНБ.
3) Рассмот. L{f1, …, fm}. Заметим, что L{f1, …, fm}∈ L{f1, …, fm-1, fm}. Пусть 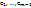 – ОНБ в лин. обл. L{f1, …, fm-1}. Строим ОНБ в лин. оболочке L{f1, …, fm-1, fm}.
– ОНБ в лин. обл. L{f1, …, fm-1}. Строим ОНБ в лин. оболочке L{f1, …, fm-1, fm}.
Рассмотрим вектора:
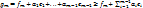 ;
;
∀k=1, …, m-1; 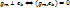
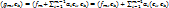 , по ∀ i ≠k.
, по ∀ i ≠k.
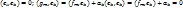
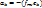
 ; g m≠0
; g m≠0
Если g m=0, то 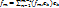 ∈ L{f1, …, fm-1}, чего быть не может.
∈ L{f1, …, fm-1}, чего быть не может.
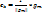 ; Ортонорм. сист.
; Ортонорм. сист. 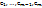 ∈ L{f1, …, fm} т.к.. dim L{f1, …, fm}=m, то
∈ L{f1, …, fm} т.к.. dim L{f1, …, fm}=m, то 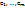 — ОНБ — процесс ортогонализации по Шмидту.
— ОНБ — процесс ортогонализации по Шмидту.
Процесс ортогонализации Грама-Шмидта
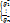 — лин. независ. вектора →
— лин. независ. вектора → 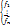 и
и 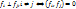
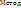
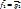
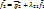 , где
, где 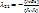 ;
;
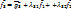 , где
, где 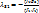 ;
; 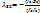 .
.
 2015-04-12
2015-04-12 848
848








