2015-04-12
694
Между квадратичными формами и симметричными билинейными формами на V $ взаимнооднозначное соответствие. F(x, y) «q(x).
Определение 8. Матрицей 
квадратичной формы q(x) в базисе [e] называется матрица полярной ей билинейной формы F(x,y) в базисе [e].
q(x) « = 
.
[e] = (e1, …, en );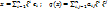 
; 
= 
;
i, j = 1, …, n.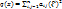 
+ 2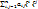 
Определение 9. Говорят, что в базисе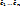 
n квадратичная форма имеет канонический вид, если q(x) = λ1(h1)2 + … + λn(hn)2, где 
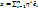. В этом случае базис [ 
] называется каноническим.
Теорема 2. (Метод Лагранжа). Пусть в некотором базисе квадратичная форма F(x, y) задаётся в виде: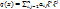 
; ( = , 
)
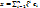Тогда в Vn $ базис [ ] = (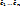) в котором квадратичная форма имеет канонический вид: q(x) = λ1(h1)2 + λ2(h2)2 + … + λn(hn)2, где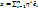
Док-во:
