Определение. Действ. квадр. матр. Q порядка n наз-ся ортогональной, если: 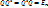 , где
, где  —матр. транспорн. к Q.
—матр. транспорн. к Q.
Св-ва ортогональных матриц
1° det Q = ±1
Док-во: 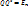 :
: 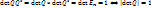
2° 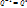 ; (Q – обратная)
; (Q – обратная)
3° Матрица А явл. ортогональной когда скалярн. квадрат кваждого столбца равен 1, а скалярн. произведение любых двух столбцов равно 0.
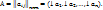
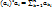 ;
; 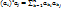 ;
;
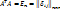 ;
; 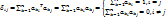
4° Св-во аналог. 3°, справедл. для строк.
5° Если матр. Q ортогон., то Q-1 тоже ортогональна.
6° Если Q, R- ортогональны, то QR – ортого.
Док-во:
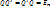
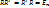
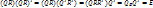
Переход от одного базиса к другому
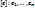 — ОНБ
— ОНБ
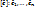 — ОНБ
— ОНБ
Пусть Q – матр. перехода от базиса [e] к  , т.е..:
, т.е..: 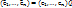
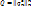 ;
; 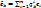 ;
; 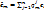
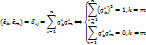
 2015-04-12
2015-04-12 743
743







