Выборочной ковариацией 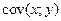 называется среднее произведений отклонений значений переменных величин
называется среднее произведений отклонений значений переменных величин 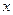 и
и 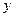 от их средних
от их средних 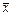 ,
, 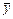 :
: 
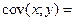
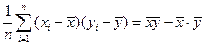 .
.
Ковариация характеризует рассеивание значений факторов 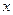 и
и 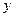 , а также линейную связь между ними:
, а также линейную связь между ними:
– при 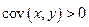 связь между факторами прямая, т.е. большим значениям x соответствуют большие значения y;
связь между факторами прямая, т.е. большим значениям x соответствуют большие значения y;
– при 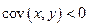 связь между факторами обратная, т.е. большим значениям x соответствуют меньшие значения y;
связь между факторами обратная, т.е. большим значениям x соответствуют меньшие значения y;
– при 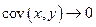 линейная связь между
линейная связь между 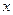 и
и 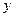 отсутствует.
отсутствует.
Более подходящим измерителем взаимосвязи переменных x и y, чем ковариация, является коэффициент корреляции 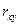 . Основная причина этого заключается в том, что ковариация зависит от единиц, в которых измеряются переменные x и y, в то время как коэффициент корреляции есть величина безразмерная.
. Основная причина этого заключается в том, что ковариация зависит от единиц, в которых измеряются переменные x и y, в то время как коэффициент корреляции есть величина безразмерная.
Линейным коэффициентом парной корреляции 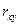 факторов
факторов 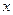 и
и 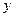 называется величина, определяемая по формуле
называется величина, определяемая по формуле
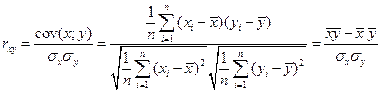 .
.
Таким образом, выборочный коэффициент корреляции устанавливает не только вид связи (прямая или обратная), но и ее силу:
1) при 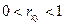 большим значениям x соответствуют большие значения y;
большим значениям x соответствуют большие значения y;
2) при 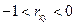 большим значениям x соответствуют меньшие значения y;
большим значениям x соответствуют меньшие значения y;
3) при 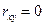 величины некоррелированы: величина коэффициента корреляции, близкая к нулю, говорит об отсутствии линейной связи между величинами, но не об отсутствии связи между ними вообще;
величины некоррелированы: величина коэффициента корреляции, близкая к нулю, говорит об отсутствии линейной связи между величинами, но не об отсутствии связи между ними вообще;
4) при 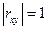 существует линейная функциональная зависимость между выборочными значениями
существует линейная функциональная зависимость между выборочными значениями 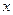 и
и 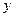 (прямая или обратная); точки лежат точно на прямой.
(прямая или обратная); точки лежат точно на прямой.
Коэффициент корреляции 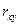 и другие характеристики регрессии определяются на основе конечного числа статистических данных (в нашем случае на основе выборки из n наблюдений). Естественно, возникает вопрос, в какой мере надежным является вывод о зависимости между переменными, сделанный только по одной выборке. Для ответа на этот вопрос применяется аппарат проверки статистических гипотез.
и другие характеристики регрессии определяются на основе конечного числа статистических данных (в нашем случае на основе выборки из n наблюдений). Естественно, возникает вопрос, в какой мере надежным является вывод о зависимости между переменными, сделанный только по одной выборке. Для ответа на этот вопрос применяется аппарат проверки статистических гипотез.
При этом в случае линейного коэффициента корреляции оценка тесноты связи между величинами на основе выборочных данных проводится согласно следующему алгоритму.
1. Рассчитывается выборочный коэффициент корреляции 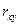 . Рассчитывается стандартная ошибка выборочного коэффициента корреляции по формуле
. Рассчитывается стандартная ошибка выборочного коэффициента корреляции по формуле 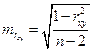 .
.
2. Проверяется значимость коэффициента корреляции, т.е. существенно ли 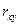 отличается от нуля или это отличие можно приписать влиянию случайности, связанной с выборкой. Для этого выдвигается нулевая гипотеза о равенстве нулю теоретического коэффициента корреляции
отличается от нуля или это отличие можно приписать влиянию случайности, связанной с выборкой. Для этого выдвигается нулевая гипотеза о равенстве нулю теоретического коэффициента корреляции 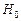 :
: 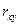 = 0 при альтернативной гипотезе:
= 0 при альтернативной гипотезе: 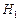 :
: 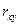
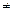 0. При проверке нулевой гипотезы используется
0. При проверке нулевой гипотезы используется 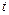 -статистика
-статистика 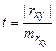 , где
, где 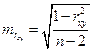 – стандартная ошибка коэффициента корреляции.
– стандартная ошибка коэффициента корреляции. 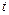 -статистика имеет распределение Стьюдента с
-статистика имеет распределение Стьюдента с 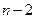 степенями свободы, где n – объем выборки. По выборке находится наблюдаемое значение статистики
степенями свободы, где n – объем выборки. По выборке находится наблюдаемое значение статистики 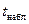 . Для заданного уровня значимости
. Для заданного уровня значимости 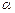 по таблице критических точек Стьюдента определяется критическая точка
по таблице критических точек Стьюдента определяется критическая точка 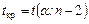 . Если
. Если 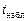
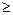
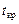 , то нулевая гипотеза об отсутствии корреляционной зависимости величин отвергается, т.е. линейный коэффициент корреляции значим и статистическая зависимость между величинами существует. Если
, то нулевая гипотеза об отсутствии корреляционной зависимости величин отвергается, т.е. линейный коэффициент корреляции значим и статистическая зависимость между величинами существует. Если 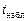 <
< 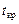 , то нулевая гипотеза принимается.
, то нулевая гипотеза принимается.
3. Для значимого коэффициента корреляции 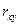 устанавливается доверительный интервал при уровне значимости
устанавливается доверительный интервал при уровне значимости 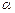 , который имеет вид:
, который имеет вид:
(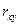 –
– 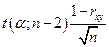 ;
; 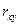 +
+ 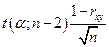 ).
).
Для определения степени взаимосвязи результативного признака с фактором необходимо знать следующие дисперсии:
5. общую дисперсию результативного признака, отображающую влияние как основного, так и неучтенных факторов: 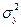
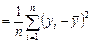 , где
, где 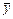 – выборочное среднее значение результативного признака по выборке
– выборочное среднее значение результативного признака по выборке 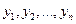 ;
;
6. факторную дисперсию результативного фактора, отражающую влияние только основного фактора: 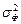
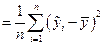 , где
, где 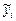
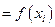 ,
, 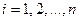 , – значения результативного признака, полученные по уравнению регрессии;
, – значения результативного признака, полученные по уравнению регрессии;
7. остаточную дисперсию результативного признака, отражающую влияние неучтенных факторов и характеризующую меру разброса зависимой переменной вокруг линии регрессии:
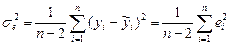 ,
,
где 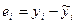 – оценки случайного члена
– оценки случайного члена 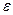 регрессии в i -ом наблюдении.
регрессии в i -ом наблюдении.
При корреляционной связи результативного фактора и объясняющих факторов выполняется соотношение: 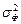
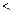
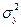 , при этом
, при этом 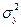 =
= 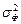 +
+ 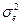 .
.
Величина 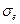 называется стандартной ошибкой регрессии (остаточным стандартным отклонением).
называется стандартной ошибкой регрессии (остаточным стандартным отклонением).
Степень взаимосвязи результативного признака с фактором в случае нелинейной регрессии оценивает индекс корреляции 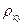 (0
(0 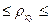 1):
1):
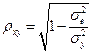
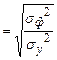 .
.
Чем ближе 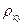 к единице, тем теснее связь рассматриваемых признаков и тем надежнее полученное уравнение регрессии. В случае нелинейной регрессии линейный коэффициент корреляции
к единице, тем теснее связь рассматриваемых признаков и тем надежнее полученное уравнение регрессии. В случае нелинейной регрессии линейный коэффициент корреляции 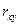 дает приближенную оценку связи и не совпадает с индексом корреляции
дает приближенную оценку связи и не совпадает с индексом корреляции 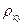 .
.
 2015-04-17
2015-04-17 2816
2816
