2015-04-17
1515
Для анализа общего качества уравнения линейной парной регрессии обычно используется коэффициент детерминации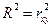 
. В случае нелинейной регрессии используется индекс детерминации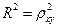 
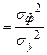. Коэффициент и индекс детерминации определяют долю разброса результативного признака, обусловленную изменением факторного признака.
Так как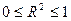 
, то величина 
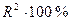в процентах показывает, какая часть изменения зависимой переменной y определяется объясняющей переменной x, а какая – другими случайными факторами.
При достаточно близком к единице коэффициенте детерминации не всегда наблюдается тесная взаимосвязь между факторами. Поэтому необходимы дополнительные исследования.
В большинстве случаев уравнение регрессии строится на основе выборочных данных. Поэтому возникает вопрос о согласованности построенного уравнения генеральной совокупности. Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным. Выдвигается гипотеза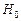 
: 
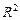= 0 о незначимости коэффициента детерминации при альтернативной гипотезе 
: 
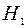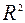
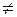0.
При проверке нулевой гипотезы используется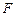 
-статистика
= 
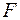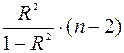, (3)
имеющая распределение Фишера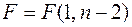 
, где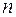 
– число наблюдений.
По выборочным данным по формуле (3.3) вычисляется наблюдаемое значение статистики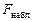 
. По таблицам критических точек 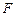-распределения находится критическое значение статистики 
= 
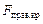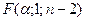при заданном уровне значимости 
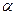. Если 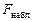попадает в критическую область, т.е.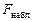 
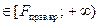, то нулевая гипотеза отвергается, что говорит о соответствии теоретического уравнения регрессии выборочным данным. Если < 
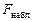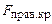, то признается ненадежность уравнения регрессии.
Для оценки адекватности уравнения регрессии также используется показатель средней ошибки аппроксимации:
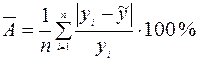
– среднее отклонение расчетных значений от фактических, допустимый предел которого не более 8 – 12 %.
Средний коэффициент эластичности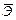 
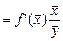на основании вида уравнения 
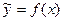парной регрессии позволяет определить, на сколько процентов в среднем по совокупности изменится результирующий фактор y при изменении фактора x на 1 % от своего номинального значения. В случае линейной регрессии = 
.
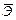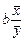Возможна ситуация, когда часть вычисленных коэффициентов парной регрессии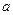 
, 
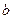не обладает необходимой степенью значимости. В этом случае такие коэффициенты должны быть исключены из уравнения регрессии. Поэтому проверка адекватности построенного уравнения регрессии наряду с проверкой значимости коэффициента детерминации 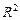включает в себя также и проверку значимости каждого коэффициента регрессии.
Для этого выдвигаются нулевые гипотезы о незначимом отличии от нуля коэффициентов регрессии а, b, т.е.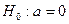 
, 
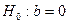при альтернативных гипотезах 
, 
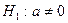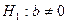. Проверка данных гипотез осуществляется с помощью 
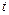-статистики, имеющей распределение Стьюдента с числом степеней свободы 
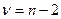. Для этого рассчитываются стандартные ошибки коэффициентов регрессии
, 
.
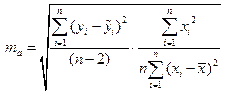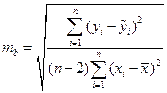По выборочным данным вычисляется наблюдаемое значение 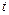-статистики 
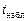как отношение значения коэффициента к величине его стандартной ошибки: 
, 
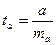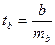, которое затем сравнивается с табличным 
= 
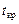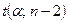. Если 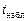попадает в критическую область, т.е.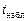 
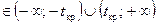, то нулевые гипотезы : 
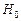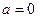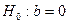, отвергаются.
Если незначимым окажется коэффициент 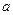, то проводится пересчет уравнения регрессии в предположении, что а = 0. Если незначимым окажется коэффициент b, то нужно изменить спецификацию модели.
Доверительные интервалы для каждого коэффициента регрессии имеют вид:
, 
.
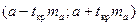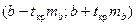Они определяют пределы, в которых находятся точные значения коэффициентов регрессии с заданным уровнем значимости.
Точечный прогноз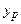 
результирующего признака y определяется путем подстановки в уравнение регрессии 
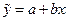значение xp независимого фактора x: 
.
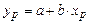Интервальный прогноз заключается в построении доверительного интервала, с заданной вероятностью покрывающего истинное значение прогноза. Предварительно рассчитывается стандартная ошибка прогноза: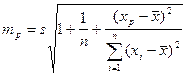 
, где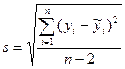 
.
Затем строится доверительный интервал прогноза
.
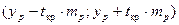Литература:
1. Елисеева И.И. Эконометрика: учебник. М.: Финансы и статистика, 2008.
2. Бородич С.А. Эконометрика: учебное пособие. Мн.: Новое знание, 2001.
3. Новиков А.И. Эконометрика: учебное пособие. М.: ИНФА-М, 2008.
4. Кремер Н.Ш. Эконометрика: учебник для студентов вузов. М.: ЮНИТИ-ДАНА, 2008.
